【题目】为了美化学习环境,加强校园绿化建设,某校计划用不多于5200元的资金购买A、B两种树苗共60棵(可以是同一种树苗),加强校园绿化建设.若购买A种树苗x棵,所需总资金为y元,A、B两种树苗的相关信息如表:
项目 | 单价(元/棵) | 成活率 |
A | 100 | 98% |
B | 60 | 90% |
(1)求y与x之间的函数关系式;
(2)若要使得所购买树苗的成活率不低于95%,有几种选购方案?所用的资金分别是多少?
参考答案:
【答案】
(1)解:y=100x+60(60﹣x)=40x+3600
100x+60(60﹣x)≤5200,
解得x≤40,
(∴0≤x≤40,且x为整数)
(2)解:98%x+90%(60﹣x)≥95%×60,
解得: ![]() ,
,
又∵x≤40,x是整数∴x=38、39、40.
所以有三种购树苗方案:①购A种树苗38棵、B种树苗22棵,所用资金38×100+22×60=5120元;②购A种树苗39棵、B种树苗21棵,所用资金39×100+21×60=5160元;③购A种树苗40棵、B种树苗20棵,所用资金为40×100+20×60=5200元
【解析】(1)总资金y=A树苗所需要的资金+B树苗所需要的资金;(2)关系式为:A种树木的成活数量+B种树木的成活数量≥树苗总数×95%,结合(1)中得到的自变量取值即可得到相应的选购方案及所用资金.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作BC的平行线交于BE的延长线于点F,且AF=DC,连接CF.
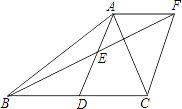
(1)求证:D是BC的中点;
(2)如果AB=AC,试判断四边形ADCF的形状,并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OB,AB分别表示甲乙两名同学运动的一次函数图象,图中s与t分别表示运动路程和时间,已知甲的速度比乙快,下列说法:①射线AB表示甲的路程与时间的函数关系;②甲的速度比乙快1.5米/ 秒;③甲比乙先跑12米;④8秒钟后,甲超过了乙,其中正确的有_____________.(填写你认为所有正确的答案序号)
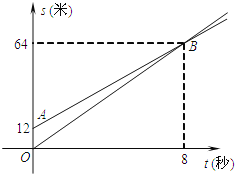
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市各学校九年级学生在体育测试前,都在积极训练自己的考试项目,王强就本班同学“自己选测的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:

(1)该班共有名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“排球”部分所对应的圆心角度数为;
(4)若全校有360名学生,请计算出全校“其他”部分的学生人数. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了参观上海世博会,某公司安排甲、乙两车分别从相距300千米的上海、泰州两地同时出发相向而行,甲到泰州带客后立即返回,下图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图像.

(1)请直接写出甲离出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量x的取值范围;
(2)当它们行驶4.5小时后离各自出发点的距离相等,求乙车离出发地的距离y(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量x的取值范围;
(3)在(2)的条件下,甲、乙两车从各自出发地驶出后经过多少时间相遇? -
科目: 来源: 题型:
查看答案和解析>>【题目】某市推出了电脑上网包月月制,每月收取费用y(元)与上网时间x(小时)之间的函数关系式如图所示,其中OA是线段,AC是射线.
(1)当x≥30时,求y与x之间的函数关系式;
(2)若小李4月份上网时间为20小时,他应付多少元上网费用;
(3)若小李5月份上网费用为75元,则他在5月份的上网时间是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,O为平面直角坐标系的原点,半径为1的⊙B经过点O,且与x,y轴分交于点A,C,点A的坐标为(﹣
 ,0),AC的延长线与⊙B的切线OD交于点D.
,0),AC的延长线与⊙B的切线OD交于点D.
(1)求OC的长和∠CAO的度数;
(2)求过D点的反比例函数的表达式.
相关试题

