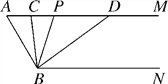
【题目】如图,已知AM∥BN,∠A=60°,点P是射线AM上一动点(与A不重合),BC、BD分别平分∠ABP和∠PBN,分别交射线AM于点C、D.
(1)求∠CBD的度数;
(2)当点P运动时,∠APB∶∠ADB的度数比值是否发生变化?若不变,请求出这个比值;若变化,请找出变化规律;
(3)当点P运动到使∠ACB=∠ABD时,求∠ABC的度数.
参考答案:
【答案】(1)60°;(2)不变,∠APB∶∠ADB=2∶1.,理由见解析;(3)∠ABC=30°
【解析】(1)由平行线的性质可求得∠ABN,再根据角平分线的定义和整体思想可求得∠CBD;
(2)由平行线的性质可得∠APB=∠PBN,∠ADB=∠DBN,再由角平分线的定义可求得结论;
(3)由平行线的性质可得到∠ACB=∠CBN,结合条件可得到∠DBN=∠ABC,且∠ABC+∠DBN=60°,可求得∠ABC的度数.
解:(1)∵AM∥BN,∠A=60°,
∴∠ABN=180°-60°=120°,
∴∠ABP+∠PBN=120°.
∵BC平分∠ABP,BD平分∠PBN,
∴∠ABP=2∠CBP,∠PBN=2∠DBP,
∴2∠CBP+2∠DBP=120°,
∴∠CBD=∠CBP+∠DBP=60°.
(2)不变,∠APB∶∠ADB=2∶1.理由如下,
∵AM∥BN,
∴∠APB=∠PBN,∠ADB=∠DBN.
∵BD平分∠PBN,
∴∠PBN=2∠DBN,
∴∠APB∶∠ADB=2∶1.
(3)∵AM∥BN,
∴∠ACB=∠CBN,
当∠ACB=∠ABD时,
则有∠CBN=∠ABD,
∴∠ABC+∠CBD=∠CBD+∠DBN,
∴∠ABC=∠DBN.
由(1)可知∠ABN=120°,∠CBD=60°,
∴∠ABC+∠DBN=60°,
∴∠ABC=30°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,CD⊥AB,EF⊥AB,垂足分别为D、F,∠1=∠2,
(1)试判断DG与BC的位置关系,并说明理由.
(2)若∠A=70°,∠BCG=40°,求∠AGD的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人两次同时在同一家粮店购买粮食(假设两次购买粮食的单价不相同),甲每次购买
粮食100千克,乙每次购买粮食用去100元.
(1)假设
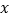 、
、 分别表示两次购买粮食时的单价(单位:元/千克),试用含
分别表示两次购买粮食时的单价(单位:元/千克),试用含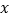 、
、 的代数式表示:甲两次购
的代数式表示:甲两次购买粮食共需付款 元,乙两次共购买 千克粮食;若甲两次购买粮食的平均单价为每千
克
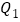 元,乙两次购买粮食的平均单价为每千克
元,乙两次购买粮食的平均单价为每千克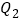 元,则
元,则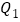 = ,
= ,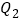 = .
= .(2)若谁两次购买粮食的平均单价低,谁购买粮食的方式就较合算.请你判断甲、乙两人购买粮食的方式哪一个较合算,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:E、F分别是AB和CD上的点,DE、AF分别交BC于点G、H, AB∥CD,∠A=∠D,试说明:(1)AF∥ED;(2)∠BED=∠A;(3) ∠1=∠2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△ABC中,∠ABC与∠ACB的平分线相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,作△ABC外角∠MBC,∠NCB的角平分线交于点Q,试探索∠Q、∠A之间的数量关系.
(3)如图③,延长线段BP、QC交于点E,△BQE中,存在一个内角等于另一个内角的2倍,求∠A的度数.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O直径AB和弦CD相交于点E,AE=2,EB=6,∠DEB=30°,求弦CD长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:
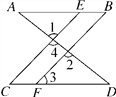
∵∠1=∠2(已知),且∠1=∠4(____________),
∴∠2=∠4(等量代换),
∴CE∥BF(__________________________),
∴∠________=∠3(______________________).
又∵∠B=∠C(已知),
∴∠3=∠B(等量代换).
∴AB∥CD(__________________________).
相关试题

