【题目】如图,AB是⊙O的直径,![]() ,∠COD=60°.
,∠COD=60°.
(1)△AOC是等边三角形吗?请说明理由;
(2)求证:OC∥BD.

参考答案:
【答案】(1)是(2)证明见解析
【解析】
试题分析:(1)由等弧所对的圆心角相等推知∠1=∠COD=60°;然后根据圆上的点到圆心的距离都等于圆的半径知OA=OC,从而证得△AOC是等边三角形;
(2)证法一:利用同垂直于一条直线的两条直线互相平行来证明OC∥BD;
证法二:通过证明同位角∠1=∠B,推知OC∥BD.
试题解析:(1)△AOC是等边三角形
证明:∵![]() ,
,
∴∠1=∠COD=60°
∵OA=OC(⊙O的半径),
∴△AOC是等边三角形;
(2)证法一:∵![]() ,
,
∴OC⊥AD
又∵AB是⊙O的直径,
∴∠ADB=90°,即BD⊥AD
∴OC∥BD
证法二:∵![]() ,
,
∴∠1=∠COD=![]() ∠AOD
∠AOD
又∠B=![]() ∠AOD
∠AOD
∴∠1=∠B
∴OC∥BD

-
科目: 来源: 题型:
查看答案和解析>>【题目】若一件商品按成本价提高40%后标价,又以8折优惠卖出,结果仍可获利15元,则这件商品的成本价为______元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:b是最大的负整数,且a,b,c满足|a+b|+(4﹣c)2016=0,试回答问题:
(1)请直接写出a,b,c的值;
(2)若a,b,c所对应的点分别为A,B,C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0≤x≤1),请化简式子:|x+1|﹣|1﹣x|+2|x﹣4|;
(3)在(1)、(2)的条件下,点A,B,C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和C分别以每秒3个单位长度和8个单位长度的速度向右运动,假设t秒后,若点B与点C之间的距离表示为BC,点A与B之间的距离表示为AB.请问:AB﹣BC的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某商店销售富硒农产品,今年1月开始盈利,2月份盈利240000元,4月份盈利290400元,且从2月份到4月份,每月盈利的平均增长率相同,则每月盈利的平均增长率是( )
A. 8%B. 9%C. 10%D. 11%
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的箱子里装有红色、蓝色、黄色的球共20个,除颜色外,形状、大小、质地等完全相同,小明通过多次摸球实验后发现摸到红色、黄色球的频率分别稳定在10%和15%,则箱子里蓝色球的个数很可能是 个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年是具有里程碑意义的一年,我们将全面建成小康社会,全面建设小康社会的基本标准包括:人均国内生产总值超过3000美元、城镇居民人均可支配收入1.8万元等十个方面.数据“1.8万元”用科学技术法表示为( ).
A.1.8×103元B.1.8×104元C.0.18×105元D.18000元
-
科目: 来源: 题型:
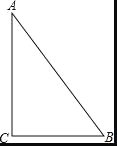
查看答案和解析>>【题目】如图,要在一块形状为直角三角形(∠C 为直角)的铁皮上裁出一个半圆形的铁皮,需先在这块铁皮画出一个半圆,使它的圆心在线段AC 上,且与AB、BC 都相切.
(1)请你用直尺和圆规作出该半圆(要求保留作图痕迹,不要求写做法)
(2)若AC=4,BC=3,求半圆的半径.
相关试题

