【题目】为增强环保意识,某社区计划开展一次“减碳环保,减少用车时间”的宣传活动,对部分家庭五月份的平均每天用车时间进行了一次抽样调查,并根据收集的数据绘制了下面两幅不完整的统计图.请根据图中提供的信息,解答下列问题:
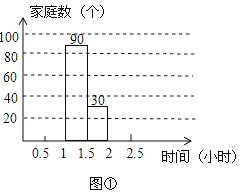
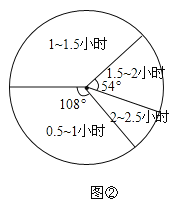
(1)本次抽样调查了多少个家庭?
(2)将图①中的条形图补充完整,直接写出用车时间的中位数落在哪个时间段内;
(3)求用车时间在1~1.5小时的部分对应的扇形圆心角的度数;
(4)若该社区有车家庭有1600个,请你估计该社区用车时间不超过1.5小时的约有多少个家庭?
参考答案:
【答案】(1)200 (2)条形图为
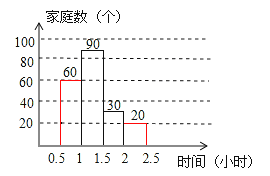
用车时间的中位数落在1~1.5小时时间段内(3)162° (4)1200
【解析】试题分析:(1)根据扇形统计图计算出用车时间在1.5-2小时所占的百分比,用1.5-2小时的频数除以其所占的百分比即可求得抽样调查的人数;
(2)根据扇形统计图分别计算出用车时间在0.5-1小时,2-2.5小时所占的百分比,用求得抽样调查的人数分别乘以用车时间在0.5-1小时,2-2.5小时所占的百分比求出每个小组的频数即可补全统计图;
(3)用人数除以总人数乘以360°即可求得圆心角的度数;
(4)用总人数乘以不超过1.5小时的所占的百分比即可.
试题解析:(1)抽查的家庭总个数为30÷![]() =200个;
=200个;
(2)用车时间在0.5~1小时的有200×![]() =60个;
=60个;
用车时间在2~2.5小时的有200﹣60﹣30﹣90=20个,统计图为下图①;
用车时间的中位数落在1~1.5小时的时间段内.
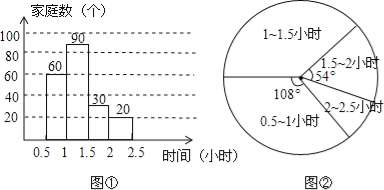
(3)用车时间在1~1.5小时的部分对应的扇形圆心角的度数为![]() ×360°=162°;
×360°=162°;
(4)该社区用车时间不超过1.5小时的约有1600×![]() =1200个;
=1200个;
-
科目: 来源: 题型:
查看答案和解析>>【题目】⊙O的半径r=5cm,圆心到直线l的距离OM=4cm,在直线l上有一点P,且PM=3cm,则点P在⊙O_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有三张正面分别写有数字-2,-1,1的卡片,它们的背面完全相同,将这三张卡片背面朝上洗匀后随机抽取一张,以其正面的数字作为x的值。放回卡片洗匀,再从三张卡片中随机抽取一张,以其正面的数字作为y的值,两次结果记为(x,y)。
(1)用树状图或列表法表示(x,y)所有可能出现的结果;
(2)若(x,y)表示平面直角坐标系中的点,求点(x,y)在函数
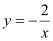 图象上的概率。
图象上的概率。 -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题3+3+4+4分)如图,在平面直角坐标系中,抛物线
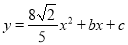 经过点A(
经过点A(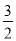 ,0)和点B(1,
,0)和点B(1,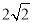 ),与x轴的另一个交点为C,
),与x轴的另一个交点为C,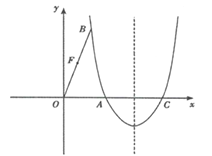
(1)求抛物线的表达式;(2)点D在对称轴的右侧,x轴上方的抛物线上,且
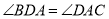 ,求点D的坐标;
,求点D的坐标;(3)在(2)的条件下,连接BD,交抛物线对称轴于点E,连接AE
①判断四边形OAEB的形状,并说明理由;
②点F是OB的中点,点M是直线BD上的一个动点,且点M与点B不重合,当
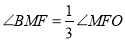 ,请直接写出线段BM的长。
,请直接写出线段BM的长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内接于⊙O,∠B=60°,CD是⊙O的直径,点P是CD延长线上的一点,且AP=AC.
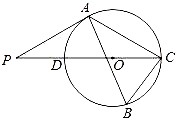
(1)求证:PA是⊙O的切线;
(2)若⊙O的半径为3,求阴影部分的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分12分)快、慢两车分别从相距480千米路程的甲、乙两地同时出发,匀速行驶,先相向而行,途中慢车因故停留1小时,然后以原速继续向甲地行驶,到达甲地后停止行驶;快车到达乙地后,立即按原路原速返回甲地(快车掉头的时间忽略不计),快、慢两车距乙地的路程
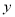 (千米)与所用时间
(千米)与所用时间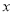 (小时)之间的函数图象如图,请结合图象信息解答下列问题:
(小时)之间的函数图象如图,请结合图象信息解答下列问题: (1)求慢车的行驶速度和
 的值;
的值; (2)求快车与慢车第一次相遇时,距离甲地的路程是多少千米?
(3)求两车出发后几小时相距的路程为
 千米?
千米? 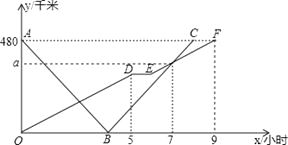
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2经过点A(2,4),求该抛物线的解析式.
相关试题

