搜索
【题目】如图，在矩形ABCD中，将△ABD沿AB向下平移使A点到达B点，得到△BEC，下列说法正确的是（ ）
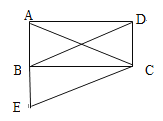
A. △ACE一定是等腰三角形B. △ACE一定是等边三角形
C. △ACE一定是锐角三角形D. △ACE不可能是等腰直角三角形
参考答案：
【答案】A
【解析】
根据矩形对角线相等的性质和平移的性质进行判断即可.
解：∵四边形ABCD是矩形，
∴AC=BD.
又△BEC是由△ABD沿AB向下平移得到的，
∴BD=EC.
∴AC=EC，
∴△ACE一定是等腰三角形.
故A正确；
AE、AC不一定相等，所以△AEC不一定是等边三角形，故B错误；
当AD=CD时，矩形ABCD是正方形，则∠ACE=90°，即△ACE是等腰直角三角形，否则不成立，所以C、D错误；
故选A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店销售A型和B型两种电脑，其中A型电脑每台的利润为400元，B型电脑每台的利润为500元．该商店计划再一次性购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的2倍，设购进A型电脑x台，这100台电脑的销售总利润为y元．
（1）求y关于x的函数关系式；
（2）该商店购进A型、B型电脑各多少台，才能使销售总利润最大，最大利润是多少？
（3）实际进货时，厂家对A型电脑出厂价下调a（0＜a＜200）元，且限定商店最多购进A型电脑60台，若商店保持同种电脑的售价不变，请你根据以上信息，设计出使这100台电脑销售总利润最大的进货方案．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知：如图，一次函数y＝
x+3的图象分别与x轴、y轴相交于点A、B，且与经过点C（2，0）的一次函数y＝kx+b的图象相交于点D，点D的横坐标为4，直线CD与y轴相交于点E．
（1）直线CD的函数表达式为 ；（直接写出结果）
（2）点Q为线段DE上的一个动点，连接BQ．
①若直线BQ将△BDE的面积分为1：2两部分，试求点Q的坐标；
②点Q是否存在某个位置，将△BQD沿着直线BQ翻折，使得点D恰好落在直线AB下方的坐标轴上？若存在，求点Q的坐标；若不存在，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了参加学校举行的传统文化知识竞赛，某班进行了四次模拟训练，将成绩优秀的人数和优秀率绘制成如下两个不完整的统计图：
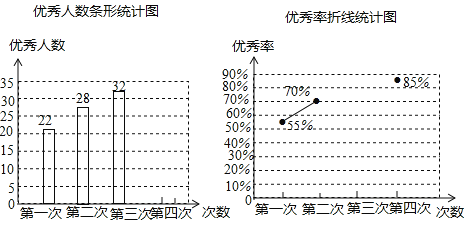
（1）求该班总人数；
（2）根据计算，请你补全两个统计图；
（3）已知该班甲同学四次训练成绩为85，95，85，95，乙同学四次成绩分别为85，90，95，90，现需从甲、乙两同学中选派一名同学参加校级比赛，你认为应该选派哪位同学并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，李强在教学楼的点P处观察对面的办公大楼，为了求得对面办公大楼的高度，李强测得办公大楼顶部点A的仰角为30°，测得办公大楼底部点B的俯角为37°，已知测量点P到对面办公大楼上部AD的距离PM为30m，办公大楼平台CD=10m．求办公大楼的高度（结果保留整数）．（参考数据：sin37°≈
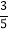，tan37°≈
，
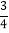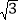≈1.73）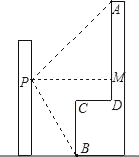
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，O为AC的中点，过点O的直线分别与AB，CD交于点E，F，连接BF交AC于点M，连接DE，BO.若∠COB＝60°，FO＝FC，则下列结论：①FB⊥OC，OM＝CM；②△EOB≌△CMB；③四边形EBFD是菱形；④MB∶OE＝3∶2.其中正确结论的个数是（ ）
A. 1 B. 2 C. 3 D. 4
-
科目： 来源： 题型：
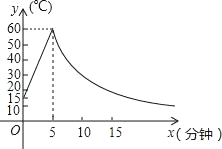
查看答案和解析>>【题目】如图为某种材料温度y（℃）随时间x（min）变化的函数图象．已知该材料初始温度为15℃，温度上升阶段y与时间x成一次函数关系，且在第5分钟温度达到最大值60℃后开始下降；温度下降阶段，温度y与时间x成反比例关系．
（1）分别求该材料温度上升和下降阶段，y与x间的函数关系式；
（2）根据工艺要求，当材料的温度高于30℃时，可以进行产品加工，问可加工多长时间？
相关试题
