【题目】如图,直线AB,CD相交于点O,OF平分∠AOE,OF⊥CD,垂足为O. 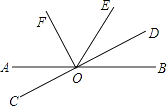
(1)写出图中所有与∠AOD互补的角;
(2)若∠AOE=120°,求∠BOD的度数.
参考答案:
【答案】
(1)解:∵直线AB,CD相交于点O,
∴∠AOC和∠BOD与∠AOD互补,
∵OF平分∠AOE,
∴∠AOF=∠EOF,
∵OF⊥CD,
∴∠COF=∠DOF=90°,
∴∠DOE=∠ACO,
∴∠DOE也是∠AOD的补角,
∴与∠AOD互补的角有∠AOC,∠BOD,∠DOE
(2)解:∵OF平分∠AOE,
∴∠AOF= ![]() ∠AOE=60°,
∠AOE=60°,
∵OF⊥CD,
∴∠COF=90°,
∴∠AOC=∠COF﹣∠AOF=90°﹣60°=30°,
∵∠AOC与∠BOD是对顶角,
∴∠BOD=∠AOC=30°
【解析】(1)根据邻补角的定义确定出∠AOC和∠BOD,再根据角平分线的定义可得∠AOF=∠EOF,根据垂直的定义可得∠COF=∠DOF=90°,然后根据等角的余角相等求出∠DOE=∠ACO,从而最后得解;(2)根据角平分线的定义求出∠AOF,再根据余角的定义求出∠AOC,然后根据对顶角相等解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读第(1)题的解答过程,然后再解第(2)题.
(1)已知多项式2x3﹣x2+m有一个因式是2x+1,求m的值.
解法一:设2x3﹣x2+m=(2x+1)(x2+ax+b),则:2x3﹣x2+m=2x3+(2a+1)x2+(a+2b)x+b
比较系数得:
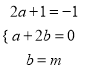 ,解得:
,解得:  ,∴
,∴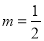 .
.解法二:设2x3﹣x2+m=A(2x+1)(A为整式)
由于上式为恒等式,为方便计算了取
 ,
, 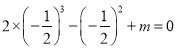 ,故
,故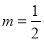 .
.(2)已知x4+mx3+nx﹣16有因式(x﹣1)和(x﹣2),求m、n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题。
(1)计算:﹣20+4﹣1×( )﹣2;
)﹣2;
(2)计算:(﹣2a2b)3÷(﹣ab)( a2b3).
a2b3). -
科目: 来源: 题型:
查看答案和解析>>【题目】(本题满分8分)2014年12月28日“青烟威荣”城际铁路正式开通,从烟台到北京的高铁里程比普快里程缩短了81千米,运行时间减少了9小时,已知烟台到北京的普快列车里程月1026千米,高铁平均时速是普快平均时速的2.5倍.
(1)求高铁列车的平均时速;
(2)某日王老师要去距离烟台大约630千米的某市参加14:00召开的会议,如果他买到
当日8:40从烟台到该是的高铁票,而且从该市火车站到会议地点最多需要1.5小时.试问在高铁列车准点到达的情况下他能在开会之前赶到吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂为了解工人在单位时间内加工同一种零件的技能水平,随机从50名工人加工的零件中各抽取了10个进行检测,统计出他们各自加工的合格品数是1到8这八个整数,现提供的部分信息如图.

请解答下列问题:
(1)根据上述信息,写出这50名工人加工出合格品数的众数;
(2)求这50名工人加工出的合格品数的中位数;
(3)厂方认定,工人在单位时间内加工出的合格品数不低于3件(含3件)为技能合格,否则,将接受技能再培训.已知该厂有同类工人400名,请估计该厂将接受技能再培训的人数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】用反证法证明“一个三角形中至多有一个钝角”时,应假设 .
-
科目: 来源: 题型:
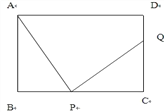
查看答案和解析>>【题目】如图,在长方形ABCD中,AB=CD=6cm,BC=10cm,点P从点B出发,以2cm/秒的速度沿BC向点C运动。设点P的运动时间为t秒,当点P从点B开始运动,同时,点Q从点C出发,沿CD向点D运动,当t =________秒时,以P、C、Q为顶点的三角形与△ABP全等。
相关试题

