【题目】已知△ABC和△ADE是等腰直角三角形,∠ACB=∠ADE=90°,点F为BE中点,连接DF、CF. 
(1)如图1,当点D在AB上,点E在AC上,请直接写出此时线段DF、CF的数量关系和位置关系(不用证明);
(2)如图2,在(1)的条件下将△ADE绕点A顺时针旋转45°时,请你判断此时(1)中的结论是否仍然成立,并证明你的判断;
(3)如图3,在(1)的条件下将△ADE绕点A顺时针旋转90°时,若AD=1,AC= ![]() ,求此时线段CF的长(直接写出结果).
,求此时线段CF的长(直接写出结果).
参考答案:
【答案】
(1)解:∵∠ACB=∠ADE=90°,点F为BE中点,
∴DF= ![]() BE,CF=
BE,CF= ![]() BE,
BE,
∴DF=CF.
∵△ABC和△ADE是等腰直角三角形,
∴∠ABC=45°
∵BF=DF,
∴∠DBF=∠BDF,
∵∠DFE=∠ABE+∠BDF,
∴∠DFE=2∠DBF,
同理得:∠CFE=2∠CBF,
∴∠EFD+∠EFC=2∠DBF+2∠CBF=2∠ABC=90°,
∴DF=CF,且DF⊥CF
(2)解:(1)中的结论仍然成立.
证明:如图,此时点D落在AC上,延长DF交BC于点G.
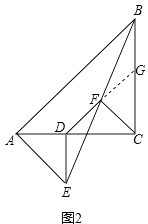
∵∠ADE=∠ACB=90°,
∴DE∥BC.
∴∠DEF=∠GBF,∠EDF=∠BGF.
∵F为BE中点,
∴EF=BF.
∴△DEF≌△GBF.
∴DE=GB,DF=GF.
∵AD=DE,
∴AD=GB,
∵AC=BC,
∴AC﹣AD=BC﹣GB,
∴DC=GC.
∵∠ACB=90°,
∴△DCG是等腰直角三角形,
∵DF=GF.
∴DF=CF,DF⊥CF
(3)解:延长DF交BA于点H,
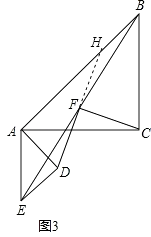
∵△ABC和△ADE是等腰直角三角形,
∴AC=BC,AD=DE.
∴∠AED=∠ABC=45°,
∵由旋转可以得出,∠CAE=∠BAD=90°,
∵AE∥BC,
∴∠AEB=∠CBE,
∴∠DEF=∠HBF.
∵F是BE的中点,
∴EF=BF,
∴△DEF≌△HBF,
∴ED=HB,
∵AC= ![]() ,在Rt△ABC中,由勾股定理,得
,在Rt△ABC中,由勾股定理,得
AB=4,
∵AD=1,
∴ED=BH=1,
∴AH=3,在Rt△HAD中由勾股定理,得
DH= ![]() ,
,
∴DF= ![]() ,
,
∴CF= ![]()
∴线段CF的长为 ![]() .
.
【解析】(1)根据“直角三角形斜边上的中线等于斜边的一半”可知DF=BF,根据∠DFE=2∠DCF,∠BFE=2∠BCF,得到∠EFD+∠EFB=2∠DCB=90°,DF⊥BF.(2)延长DF交BC于点G,先证明△DEF≌△GCF,得到DE=CG,DF=FG,根据AD=DE,AB=BC,得到BD=BG又因为∠ABC=90°,所以DF=CF且DF⊥BF.(3)延长DF交BA于点H,先证明△DEF≌△HBF,得到DE=BH,DF=FH,根据旋转条件可以△ADH为直角三角形,由△ABC和△ADE是等腰直角三角形,AC= ![]() ,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,由DF=BF,求出得CF的值.
,可以求出AB的值,进而可以根据勾股定理可以求出DH,再求出DF,由DF=BF,求出得CF的值.
【考点精析】解答此题的关键在于理解等腰直角三角形的相关知识,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°,以及对勾股定理的概念的理解,了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在3×3的正方形网格中,∠1+∠2+∠3+∠4+∠5=_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知某船于上午8时在A处观测小岛C在北偏东60°方向上,该船以每小时20海里的速度向东航行到B处,测得小岛C在北偏东30°方向上,船以原来的速度继续向东航行2小时,到达岛C正南方点D处,船从A到D一共航行了多少海里?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠B=∠D.说明AB∥CD的理由.
补全下面的说理过程,并在括号内填上适当的理由
解:∵∠1+∠2=180°(已知)
∠2=∠AHB( )
∴ (等量代换)
∴DE∥BF( )
∴∠D=∠ ( )
∵∠ =∠B(等量代换)
∴AB∥CD( )

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由.
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=ax2+bx+c(a>0)图象的顶点为D,其图象与x轴的交点A(﹣1,0)、B(3,0),与y轴负半轴交于点C.
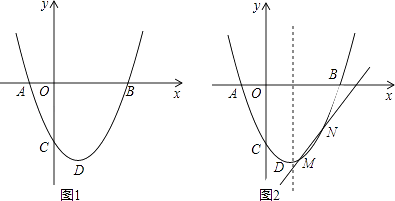
(1)若△ABD为等腰直角三角形,求此时抛物线的解析式;
(2)a为何值时△ABC为等腰三角形?
(3)在(1)的条件下,抛物线与直线y= x﹣4交于M、N两点(点M在点N的左侧),动点P从M点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点N,若使点P运动的总路径最短,求点P运动的总路径的长.
x﹣4交于M、N两点(点M在点N的左侧),动点P从M点出发,先到达抛物线的对称轴上的某点E,再到达x轴上的某点F,最后运动到点N,若使点P运动的总路径最短,求点P运动的总路径的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=1cm,BC=2cm,点P从点A出发,以1cm/s的速度沿折线AC→CB→BA运动,最终回到点A,设点P的运动时间为x(s),线段AP的长度为y(cm),则能够反映y与x之间函数关系的图象大致是( )
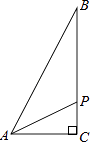
A.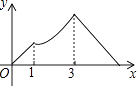
B.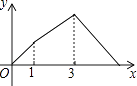
C.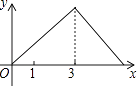
D.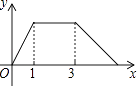
相关试题

