【题目】已知反比例函数图象经过点M(2,6)
(1)求这个函数的解析式,并指出它的图象位于哪些象限?
(2)在这个图象上任取两个点A(a,b)和B(a′,b′),如果a>a′,那么b和b′怎样的大小关系?
参考答案:
【答案】(1)y=![]() ,它的图象位于第一三象限;(2)见解析.
,它的图象位于第一三象限;(2)见解析.
【解析】
(1)设这个反比例函数解析式为y=![]() ,把点M的坐标代入解析式求出k的值即可得解,再根据反比例函数图象的性质解答即可;(2)分a、a′同号和异号两种情况,根据反比例函数的增减性即可解答.
,把点M的坐标代入解析式求出k的值即可得解,再根据反比例函数图象的性质解答即可;(2)分a、a′同号和异号两种情况,根据反比例函数的增减性即可解答.
(1)设这个反比例函数解析式为y=![]() ,
,
∵反比例函数图象经过点M(2,6),
∴![]() =6,
=6,
∴k=12,
∴y=![]() ,
,
∵k=12>0,
∴它的图象位于第一三象限;
(2)①a>a′>0或a′<a<0时,
∵k>0,
∴在每一个象限内,y随x的增大而减小,
∵a>a′,
∴b<b′;
②a>0>a′时,y=![]() ,
,
∵a>0,
∴b>0,
∵a′<0,
∴b′<0,
∴b>b′.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+3与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是_____.
x+3与坐标轴交于A,B两点,在射线AO上有一点P,当△APB是以AP为腰的等腰三角形时,点P的坐标是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,经过点A的双曲线y=
 (x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
(x>0)同时经过点B,且点A在点B的左侧,点A的横坐标为1,∠AOB=∠OBA=45°,则k的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点△ABC(顶点是网格线的交点),在建立的平面直角坐标系中,△ABC绕旋转中心P逆时针旋转90°后得到△A1B1C1.
(1)在图中标示出旋转中心P,并写出它的坐标;
(2)以原点O为位似中心,将△A1B1C1作位似变换且放大到原来的两倍,得到△A2B2C2,在图中画出△A2B2C2,并写出C2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形ABC(顶点是网格线的交点的三角形)的顶点B、C的坐标分别为(﹣2,0),(﹣1,2).

(1)请在如图所示的网格中根据上述点的坐标建立对应的直角坐标系;(只要画图,不需要说明)
(2)在(1)中建立的平面直角坐标系中,先画出△ABC关于y轴对称的图形△A1B1C1,再画出△A1B1C1关于x轴对称的图形△A2B2C2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】水龙头关闭不紧会造成滴水,小明用可以显示水量的容器做图①所示的试验,并根据试验数据绘制出图②所示的容器内盛水量W(L)与滴水时间t(h)的函数关系图象,请结合图象解答下列问题:
(1)容器内原有水多少?
(2)求W与t之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升?

图 ① 图②
-
科目: 来源: 题型:
查看答案和解析>>【题目】在进行二次根式化简时,我们有时会碰上如
 ,
,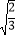 ,
, 一样的式子,这样的式子我们可以将其进一步化简
一样的式子,这样的式子我们可以将其进一步化简 =
= ,
, ,
, 以上这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:
以上这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:(1)化简:
 ;
;(2)若a是
 的小数部分,求
的小数部分,求 的值;
的值;(3)矩形的面积为3
 +1,一边长为
+1,一边长为 ﹣2,求它的周长.
﹣2,求它的周长.
相关试题

