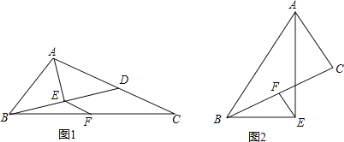
【题目】如图,在△ABC中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证:EF=![]() (AC﹣AB);
(AC﹣AB);
(2)如图2,请直接写出线段AB、AC、EF之间的数量关系。
参考答案:
【答案】(1)详见解析;(2)EF=![]() (AB-AC),理由详见解析.
(AB-AC),理由详见解析.
【解析】
(1)先证明AB=AD,根据等腰三角形的三线合一,推出BE=ED,根据三角形的中位线定理即可解决问题;
(2)先证明AB=AP,根据等腰三角形的三线合一,推出BE=ED,根据三角形的中位线定理即可解决问题.
(1)证明 如图1中,

∵AE⊥BD,
∴∠AED=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠DAE+∠ADE=90°,
∵∠BAE=∠DAE,
∴∠ABE=∠APE,
∴AB=AD,∵AE⊥BD,
∴BE=DE,∵BF=FC,
∴EF=![]() DC=
DC=![]() (AC-AD)=
(AC-AD)=![]() (AC-AB).
(AC-AB).
(2)结论:EF=![]() (AB-AC),
(AB-AC),
理由:如图2中,延长AC交BE的延长线于P.

∵AE⊥BP,
∴∠AEP=∠AEB=90°,
∴∠BAE+∠ABE=90°,∠PAE+∠APE=90°,
∵∠BAE=∠PAE,
∴∠ABE=∠ADE,
∴AB=AP,
∵AE⊥BD,
∴BE=PE,
∵BF=FC,
∴EF=![]() PC=
PC=![]() (AP-AC)=
(AP-AC)=![]() (AB-AC).
(AB-AC).
-
科目: 来源: 题型:
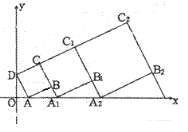
查看答案和解析>>【题目】在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1 , 作正方形A1B1C1C,延长C1B1交x轴于点A2 , 作正方形A2B2C2C1,………按这样的规律进行下去,第2012个正方形的面积为( )
A.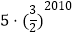
B.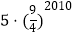
C.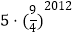
D.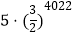
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在长方形
 中,边
中,边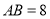 ,
,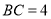 ,以点
,以点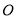 为原点,
为原点,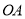 ,
,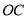 所在的直线为
所在的直线为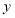 轴和
轴和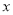 轴,建立直角坐标系.
轴,建立直角坐标系.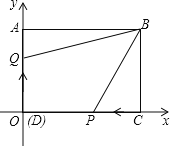
(1)点
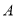 的坐标为
的坐标为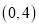 ,则
,则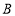 点坐标为______,
点坐标为______,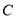 点坐标为______;
点坐标为______;(2)当点
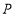 从
从 出发,以2单位/秒的速度沿
出发,以2单位/秒的速度沿 方向移动(不过
方向移动(不过 点),
点), 从原点
从原点 出发以1单位/秒的速度沿
出发以1单位/秒的速度沿 方向移动(不过
方向移动(不过 点),
点), ,
, 同时出发,在移动过程中,四边形
同时出发,在移动过程中,四边形 的面积是否变化?若不变,求其值;若变化,求其变化范围.
的面积是否变化?若不变,求其值;若变化,求其变化范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,OP平分∠AOB,∠AOP=15°,PC∥OA,PD⊥OA于点D,PC=4,则PD的长为( )

A. 2 B. 3 C. 4 D. 2
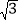
-
科目: 来源: 题型:
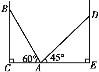
查看答案和解析>>【题目】如图,在两面墙之间有一个底端在A点的梯子,当它靠在一侧墙上时,梯子的顶端在B点;当它靠在另一侧墙上时,梯子的顶端在D点.已知∠BAC=60°,∠DAE=45°,点D到地面的垂直距离DE=3 m.
(1)求两面墙之间距离CE的大小;
(2)求点B到地面的垂直距离BC的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,AD=6,DC=8,菱形EFGH的三个顶点E、G、H分別在矩形ABCD的边AB、CD、DA上,AH=2.
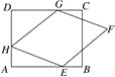
(1)已知DG=6,求AE的长;
(2)已知DG=2,求证:四边形EFGH为正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若
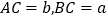 ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:(1)试说明
 ;
;(2)如果大正方形的面积是10,小正方形的面积是2,求
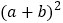 的值.
的值.
相关试题

