【题目】用配方法解下列方程时,配方错误的是( )
A.x2+2x﹣99=0化为(x+1)2=100
B.![]()
C.x2+8x+9=0化为(x+4)2=25
D.![]()
参考答案:
【答案】C
【解析】解:A、由原方程,得x2+2x=99,
等式的两边同时加上一次项系数2的一半的平方1,得
(x+1)2=100;
故本选项正确;
B、由原方程,得
m2﹣7m=4,
等式的两边同时加上一次项系数﹣7的一半的平方 ![]() ,得
,得![]() ;
;
故本选项正确;
C、由原方程,得
x2+8x=﹣9,
等式的两边同时加上一次项系数8的一半的平方16,得
(x+4)2=7;
故本选项错误;
D、由原方程,得
3x2﹣4x=2,
化二次项系数为1,得
x2﹣ ![]() x=
x= ![]()
等式的两边同时加上一次项系数﹣ ![]() 的一半的平方
的一半的平方 ![]() ,得
,得![]() ;
;
故本选项正确.
故选C.
【考点精析】掌握配方法是解答本题的根本,需要知道左未右已先分离,二系化“1”是其次.一系折半再平方,两边同加没问题.左边分解右合并,直接开方去解题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣
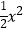 +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.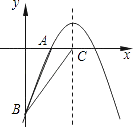
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
 ,
,  )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知A(8,0),△AOP为等腰三角形且面积为16,满足条件的P点有( )
A. 4个 B. 8个 C. 10个 D. 12个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、M在BC上,则∠EAN=_____.

-
科目: 来源: 题型:
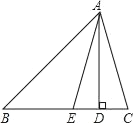
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线.
(1)若∠B=38°,∠C=70°,求∠DAE的度数;
(2)若∠B>∠C,试探求∠DAE、∠B、∠C之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)和正比例函数y=
 x的图象如图所示,则方程ax2+(b﹣
x的图象如图所示,则方程ax2+(b﹣  )x+c=0(a≠0)的两根之和( )
)x+c=0(a≠0)的两根之和( ) 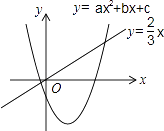
A.大于0
B.等于0
C.小于0
D.不能确定
相关试题

