【题目】平面直角坐标系中,已知A(8,0),△AOP为等腰三角形且面积为16,满足条件的P点有( )
A. 4个 B. 8个 C. 10个 D. 12个
参考答案:
【答案】C
【解析】
使△AOP为等腰三角形,只需分两种情况考虑:OA当底边或OA当腰.当OA是底边时,有2个点;当OA是腰时,有8个点,即可得出答案.
∵A(8,0),
∴OA=8,
设△AOP的边OA上的高是h,
则![]() ×8×h=16,
×8×h=16,
解得:h=4,
在x轴的两侧作直线a和直线b都和x轴平行,且到x轴的距离都等于4,如图:

①以A为圆心,以8为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,
②以O为圆心,以8为半径画弧,交直线a和直线b分别有两个点,即共4个点符合,
③作AO的垂直平分线分别交直线a、b于一点,即共2个点符合,
4+4+1+1=10.
故选C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,P、Q分别是BC、AC上的点,作PR⊥AB,PS⊥AC,垂足分别为R、S,若AQ=PQ,PR=PS,则结论:①PA平分∠RPS;②AS=AR;③QP∥AR;④△BRP≌△CSP.其中正确的有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=﹣
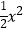 +bx+c的图象经过A(2,0)、B(0,﹣6)两点.
+bx+c的图象经过A(2,0)、B(0,﹣6)两点.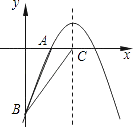
(1)求这个二次函数的解析式;
(2)设该二次函数的对称轴与x轴交于点C,连接BA、BC,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(
 ,
,  )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)求抛物线的解析式;
(2)是否存在这样的P点,使线段PC的长有最大值?若存在,求出这个最大值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】用配方法解下列方程时,配方错误的是( )
A.x2+2x﹣99=0化为(x+1)2=100
B.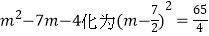
C.x2+8x+9=0化为(x+4)2=25
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在△ABC中,∠BAC=106°,EF、MN分别是AB、AC的垂直平分线,点E、M在BC上,则∠EAN=_____.

-
科目: 来源: 题型:
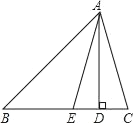
查看答案和解析>>【题目】如图,在△ABC中,AD是BC边上的高,AE是∠BAC平分线.
(1)若∠B=38°,∠C=70°,求∠DAE的度数;
(2)若∠B>∠C,试探求∠DAE、∠B、∠C之间的数量关系.
相关试题

