搜索
【题目】（1）计算：
．
（2）如图，一次函数y=x+b与反比例函数
在第一象限的图象交于点B，且点B的横坐标为1，过点B作y轴的垂线，C为垂足，若S△BCO= 
，求一次函数和反比例函数的解析式．
参考答案：
【答案】（1）
；（2）
，
．
【解析】试题分析：（1）根据实数的运算法则以及运算顺序计算即可；
（2）根据点B的横坐标是1，求出OC的长利用三角形的面积求出b值，点B的坐标即可求出，代入反比例函数即可求出k值，解析式可得．
试题解析：解：（1）原式=﹣1+3+
﹣1=1+；
（2）∵一次函数y=x+b过点B，且点B的横坐标为1，∴y=1+b，即B（1，1+b）．
∵BC⊥y轴，且S△BCO=1.5，∴
×OC×BC=×1×（b+1）=1.5，解得：b=2，∴B（1，3），∴一次函数的解析式为y=x+2．
又∵y=
过点B，∴3=
，解得：k=3，∴反比例函数的解析式为：y=
．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，AB=4，BC=6，E是BC边的中点，点P在线段AD上，过P作PF⊥AE于F，设PA=x．
（1）求证：△PFA∽△ABE；
（2）当点P在线段AD上运动时，设PA=x，是否存在实数x，使得以点P，F，E为顶点的三角形也与△ABE相似？若存在，请求出x的值；若不存在，请说明理由；
（3）探究：当以D为圆心，DP为半径的⊙D与线段AE只有一个公共点时，请直接写出x满足的条件： ．
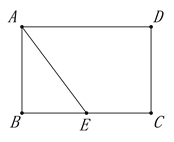
备用图
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义一种新运算：观察下列式：
1⊙3=1×4+3=7 3⊙（﹣1）=3×4﹣1=11 5⊙4=5×4+4=24 4⊙（﹣3）=4×4﹣3=13
（1）请你想一想：a⊙b= ；
（2）若a≠b，那么a⊙b b⊙a（填入“=”或“≠” ）
（3）若a⊙（﹣2b）=3，请计算 （a﹣b）⊙（2a+b）的值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在Rt△ABC中，∠C=90°，以AC为直径作⊙O，交AB于D，过点O作OE∥AB，交BC于E．
（1）求证：ED为⊙O的切线；
（2）如果⊙O的半径为
，ED=2，延长EO交⊙O于F，连接DF、AF，求△ADF的面积．
【答案】（1）证明见解析；（2）
【解析】试题分析：（1）首先连接OD，由OE∥AB，根据平行线与等腰三角形的性质，易证得
≌
即可得
，则可证得
为
的切线；
（2）连接CD，根据直径所对的圆周角是直角，即可得
利用勾股定理即可求得
的长，又由OE∥AB，证得
根据相似三角形的对应边成比例，即可求得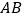
的长，然后利用三角函数的知识，求得
与
的长，然后利用S△ADF=S梯形ABEF-S梯形DBEF求得答案．试题解析：(1)证明：连接OD，
∵OE∥AB，
∴∠COE=∠CAD，∠EOD=∠ODA，
∵OA=OD,
∴∠OAD=∠ODA，
∴∠COE=∠DOE，
在△COE和△DOE中，
∴△COE≌△DOE(SAS)，
∴ED⊥OD，
∴ED是
的切线；(2)连接CD，交OE于M，
在Rt△ODE中，
∵OD=32，DE=2，
∵OE∥AB，
∴△COE∽△CAB，
∴AB=5，∵AC是直径，
∵EF∥AB，
∴S△ADF=S梯形ABEFS梯形DBEF
∴△ADF的面积为
【题型】解答题
【结束】
25【题目】【题目】已知，抛物线y=ax2+ax+b（a≠0）与直线y=2x+m有一个公共点M（1，0），且a＜b．
（1）求b与a的关系式和抛物线的顶点D坐标（用a的代数式表示）；
（2）直线与抛物线的另外一个交点记为N，求△DMN的面积与a的关系式；
（3）a=﹣1时，直线y=﹣2x与抛物线在第二象限交于点G，点G、H关于原点对称，现将线段GH沿y轴向上平移t个单位（t＞0），若线段GH与抛物线有两个不同的公共点，试求t的取值范围．
-
科目： 来源： 题型：
查看答案和解析>>【题目】 某单位在二月份准备组织部分员工到北京旅游，现联系了甲、乙两家旅行社，两家旅行社报价均为2000元/人，两家旅行社同时都对10人以上的团体推出了优惠举措：甲旅行社对每位员工七五折优惠；而乙旅行社是免去一位带队管理员工的费用，其余员工八折优惠．
(1)如果设参加旅游的员工共有a(a
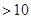)人，则甲旅行社的费用为 元，乙旅行社的费用为 元；(用含a的代数式表示，并化简．)(2)假如这个单位现组织包括管理员工在内的共20名员工到北京旅游，该单位选择哪一家旅行社比较优惠？请说明理由；
(3)如果计划在二月份外出旅游七天，设最中间一天的日期为m．
①这七天的日期之和为 ；(用含m的代数式表示，并化简.)
②假如这七天的日期之和为63的倍数，则他们可能于二月几号出发?(写出所有符合条件的可能性，并写出简单的计算过程.)
-
科目： 来源： 题型：
查看答案和解析>>【题目】检修小组从A地出发，在东西路上检修线路，若规定向东行驶的路程为正数，向西行驶的路程为负数，一天中行驶记录（单位；千米）如下：
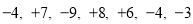
（1）收工时检修小组在A地的哪侧，距A地多远？
（2）若每千米耗油0.3升，从出发到收工共耗油多少升？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1是边长为
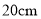的正方形薄铁片，小明将其四角各剪去一个相同的小正方形(图中阴影部分)后，发现剩余的部分能折成一个无盖的长方体盒子，图2为盒子的示意图（铁片的厚度忽略不计).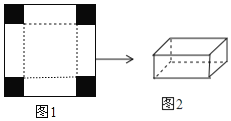
（1）设剪去的小正方形的边长为
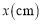，折成的长方体盒子的容积为
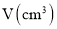, 用只含字母
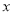的式子表示这个盒子的高为________
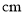，底面积为________
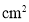，盒子的容积
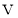为________
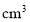；(2)为探究盒子的体积与剪去的小正方形的边长
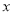之间的关系，小明列表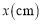1
2
3
4
5
6
7
8
_______
_______
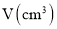
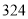
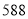
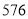
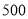
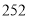
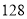
请将表中数据补充完整，并根据表格中的数据写出当
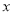的值逐渐增大时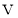，的值如何变化？
相关试题
