【题目】如图,已知△ABC中,∠C=90°,点M从点C出发沿CB方向以1cm/s的速度匀速运动,到达点B停止运动,在点M的运动过程中,过点M作直线MN交AC于点N,且保持∠NMC=45°,再过点N作AC的垂线交AB于点F,连接MF,将△MNF关于直线NF对称后得到△ENF,已知AC=8cm,BC=4cm,设点M运动时间为t(s),△ENF与△ANF重叠部分的面积为y(cm2).
(1)在点M的运动过程中,能否使得四边形MNEF为正方形?如果能,求出相应的t值;如果不能,说明理由;
(2)求y关于t的函数解析式及相应t的取值范围;
(3)当y取最大值时,求sin∠NEF的值.
参考答案:
【答案】
(1)
解:能使得四边形MNEF为正方形;理由如下:
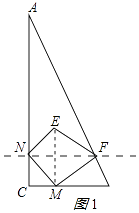
连接ME交NF于O,如图1所示:
∵∠C=90°,∠NMC=45°,NF⊥AC,
∴CN=CM=t,FN∥BC,
∴AN=8﹣t,△ANF∽△ACB,
∴ ![]() =
= ![]() =2,
=2,
∴NF= ![]() AN=
AN= ![]() (8﹣t),
(8﹣t),
由对称的性质得:∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,
∵四边形MNEF是正方形,
∴OE=ON=FN,
∴t= ![]() ×
× ![]() (8﹣t),
(8﹣t),
解得:t= ![]() ;
;
即在点M的运动过程中,能使得四边形MNEF为正方形,t的值为 ![]() ;
;
(2)
解:分两种情况:
①当0<t≤2时,y= ![]() ×
× ![]() (8﹣t)×t=﹣
(8﹣t)×t=﹣ ![]() t2+2t,
t2+2t,
即y=﹣ ![]() t2+2t(0<t≤2);
t2+2t(0<t≤2);
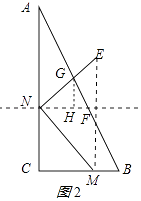
②当2<t≤4时,如图2所示:作GH⊥NF于H,
由(1)得:NF= ![]() (8﹣t),GH=NH,GH=2FH,
(8﹣t),GH=NH,GH=2FH,
∴GH= ![]() NF=
NF= ![]() (8﹣t),
(8﹣t),
∴y= ![]() NF′GH=
NF′GH= ![]() ×
× ![]() (8﹣t)×
(8﹣t)× ![]() (8﹣t)=
(8﹣t)= ![]() (8﹣t)2,
(8﹣t)2,
即y= ![]() (8﹣t)2(2<t≤4);
(8﹣t)2(2<t≤4);
(3)
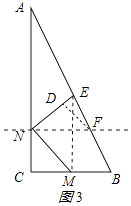
解:当点E在AB边上时,y取最大值,
连接EM,如图3所示:
则EF=BF,EM=2CN=2CM=2t,EM=2BM,
∵BM=4﹣t,
∴2t=2(4﹣t),
解得:t=2,
∴CN=CM=2,AN=6,
∴BM=4﹣2=2,NF= ![]() AN=3,
AN=3,
∴EM=2BM=4,
作FD⊥NE于D,则EB= ![]() =
= ![]() =2
=2 ![]() ,△DNF是等腰直角三角形,
,△DNF是等腰直角三角形,
∴EF= ![]() =
= ![]() ,DF=
,DF= ![]() HF=
HF= ![]() ,
,
在Rt△DEF中,sin∠NEF= ![]() =
= ![]() =
= ![]() .
.
【解析】(1)由已知得出CN=CM=t,FN∥BC,得出AN=8﹣t,由平行线证出△ANF∽△ACB,得出对应边成比例求出NF= ![]() AN=
AN= ![]() (8﹣t),由对称的性质得出∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,由正方形的性质得出OE=ON=FN,得出方程,解方程即可;(2)分两种情况:①当0<t≤2时,由三角形面积得出y=﹣
(8﹣t),由对称的性质得出∠ENF=∠MNF=∠NMC=45°,MN=NE,OE=OM=CN=t,由正方形的性质得出OE=ON=FN,得出方程,解方程即可;(2)分两种情况:①当0<t≤2时,由三角形面积得出y=﹣ ![]() t2+2t;②当2<t≤4时,作GH⊥NF于H,由(1)得:NF=
t2+2t;②当2<t≤4时,作GH⊥NF于H,由(1)得:NF= ![]() (8﹣t),GH=NH,GH=2FH,得出GH=
(8﹣t),GH=NH,GH=2FH,得出GH= ![]() NF=
NF= ![]() (8﹣t),由三角形面积得出y=
(8﹣t),由三角形面积得出y= ![]() (8﹣t)2(2<t≤4);(3)当点E在AB边上时,y取最大值,连接EM,则EF=BF,EM=2CN=2CM=2t,EM=2BM,得出方程,解方程求出CN=CM=2,AN=6,得出BM=2,NF=
(8﹣t)2(2<t≤4);(3)当点E在AB边上时,y取最大值,连接EM,则EF=BF,EM=2CN=2CM=2t,EM=2BM,得出方程,解方程求出CN=CM=2,AN=6,得出BM=2,NF= ![]() AN=3,因此EM=2BM=4,作FD⊥NE于D,由勾股定理求出EB=
AN=3,因此EM=2BM=4,作FD⊥NE于D,由勾股定理求出EB= ![]() =2
=2 ![]() ,求出EF=
,求出EF= ![]() =
= ![]() ,由等腰直角三角形的性质和勾股定理得出DF=
,由等腰直角三角形的性质和勾股定理得出DF= ![]() HF=
HF= ![]() ,在Rt△DEF中,由三角函数定义即可求出sin∠NEF的值.
,在Rt△DEF中,由三角函数定义即可求出sin∠NEF的值.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,设反比例函数的解析式为y=
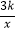 (k>0).
(k>0). 
(1)若该反比例函数与正比例函数y=2x的图象有一个交点的纵坐标为2,求k的值;
(2)若该反比例函数与过点M(﹣2,0)的直线l:y=kx+b的图象交于A,B两点,如图所示,当△ABO的面积为 时,求直线l的解析式.
时,求直线l的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB是圆O的直径,弦CD⊥AB,垂足为H,与AC平行的圆O的一条切线交CD的延长线于点M,交AB的延长线于点E,切点为F,连接AF交CD于点N.

(1)求证:CA=CN;
(2)连接DF,若cos∠DFA= ,AN=2
,AN=2  ,求圆O的直径的长度.
,求圆O的直径的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的图象的顶点坐标是(2,1),并且经过点(4,2),直线y=
 x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
x+1与抛物线交于B,D两点,以BD为直径作圆,圆心为点C,圆C与直线m交于对称轴右侧的点M(t,1),直线m上每一点的纵坐标都等于1.
(1)求抛物线的解析式;
(2)证明:圆C与x轴相切;
(3)过点B作BE⊥m,垂足为E,再过点D作DF⊥m,垂足为F,求BE:MF的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知OB=1,以OB为直角边作等腰直角三角形A1BO,再以OA1为直角边作等腰直角三角形A2A1O,如此下去,则线段OAn的长度为 .
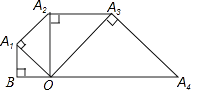
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣2)2﹣( )﹣1+20170
)﹣1+20170
(2)(1+ )÷
)÷  .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】
(1)解方程: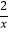 =
= 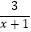
(2)解不等式组: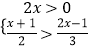 .
.
相关试题

