【题目】某学校计划购买排球、篮球,已知购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元.
(1)求购买1个排球、1个篮球的费用分别是多少元?
(2)若该学校计划购买此类排球和篮球共60个,并且篮球的数量不超过排球数量的2倍.求至少需要购买多少个排球?并求出购买排球、篮球总费用的最大值?
参考答案:
【答案】(1)每个排球的价格是60元,每个篮球的价格是120元;(2)m=20时,购买排球、篮球总费用的最大,购买排球、篮球总费用的最大值为6000元.
【解析】(1)根据购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元列出方程组,解方程组即可;
(2)根据购买排球和篮球共60个,篮球的数量不超过排球数量的2倍列出不等式,解不等式即可.
(1)设每个排球的价格是x元,每个篮球的价格是y元,
根据题意得:![]() ,
,
解得:![]() ,
,
所以每个排球的价格是60元,每个篮球的价格是120元;
(2)设购买排球m个,则购买篮球(60﹣m)个,
根据题意得:60﹣m≤2m,
解得m≥20,
又∵排球的单价小于蓝球的单价,
∴m=20时,购买排球、篮球总费用的最大,
购买排球、篮球总费用的最大值=20×60+40×120=6000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.

-
科目: 来源: 题型:
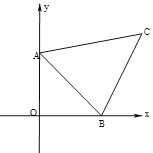
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(0,3),B(3,0),C(5,4),∠OAB=∠OBA=45°,点P为坐标系中第一象限内一点(不与C重合),若△BAP≌△ABC,则点P坐标为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:(1)△BDA≌△AEC;(2)DE=BD+CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,以△ABC的边AB、AC为腰分别向外作等腰直角三角形ABD和等腰直角三角形ACE,连接DE.若M为BC中点,MA延长线交DE于点H,
(1) 求证:AH⊥DE.
(2) 若DE=4,AH=3,求△ABM的面积

-
科目: 来源: 题型:
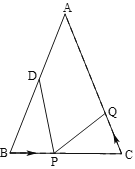
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,∠B=∠C,点D为AB的中点.
(1)如果点P在线段BC上以3cm/s的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
①若点Q的运动速度与点P的运动速度相等,经过1s后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为时________cm/s,在运动过程中能够使△BPD与△CQP全等.(直接填答案)
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(问题提出)
学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.
(初步思考)
我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.

(深入探究)
第一种情况:当∠B是直角时,△ABC≌△DEF.
(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 ,可以知道Rt△ABC≌Rt△DEF.
第二种情况:当∠B是钝角时,△ABC≌△DEF.
(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.
第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.
(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)
(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若 ,则△ABC≌△DEF.
相关试题

