【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.

参考答案:
【答案】(1)证明见解析;(2)AB=13cm,
【解析】(1)由三角形中位线定理推知ED∥FC,2DE=BC,然后结合已知条件“EF∥DC”,利用两组对边相互平行得到四边形DCFE为平行四边形;
(2)根据在直角三角形中,斜边上的中线等于斜边的一半得到AB=2DC,即可得出四边形DCFE的周长=AB+BC,故BC=25﹣AB,然后根据勾股定理即可求得;
(1)∵D、E分别是AB、AC的中点,F是BC延长线上的一点,
∴ED是Rt△ABC的中位线,
∴ED∥FC.BC=2DE,
又 EF∥DC,
∴四边形CDEF是平行四边形;
(2)∵四边形CDEF是平行四边形;
∴DC=EF,
∵DC是Rt△ABC斜边AB上的中线,
∴AB=2DC,
∴四边形DCFE的周长=AB+BC,
∵四边形DCFE的周长为25cm,AC的长5cm,
∴BC=25﹣AB,
∵在Rt△ABC中,∠ACB=90°,
∴AB2=BC2+AC2,即AB2=(25﹣AB)2+52,
解得,AB=13cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级一班开展了“读一本好书”的活动,班委会对学生阅读书籍的情况进行了问卷调查,问卷设置了“小说”“戏剧”“散文”“其他”四个选项,每位同学仅选一项,根据调查结果绘制了如下不定整的频数分布表和扇形统计图.
类别
频数(人数)
频率
小说
16
戏剧
4
散文
a
其他
b
合计
1
根据图表提供的信息,解答下列问题:
(1)直接写出a,b,m的值;
(2)在调查问卷中,甲、乙、丙、丁四位同学选择了“戏剧”类,现从以上四位同学中任意选出2名同学参加学校的戏剧兴趣小组,请用列表法或画树状图的方法,求选取的2人恰好乙和丙的概率.

-
科目: 来源: 题型:
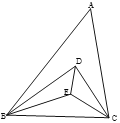
查看答案和解析>>【题目】如图,△ABC中,∠A=57°,BD、BE将∠ABC三等分,CD、CE将∠ACB三等分,则∠BDE=_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图 1,CE 平分∠ACD,AE 平分∠BAC,且∠EAC+∠ACE=90°.
(1)请判断 AB 与 CD 的位置关系,并说明理由;
(2)如图 2,若∠E=90°且 AB 与 CD 的位置关系保持不变,当直角顶点 E 移动时,写出∠BAE 与∠ECD 的数量关系,并说明理由;
(3)如图 3,P 为线段 AC 上一定点,点 Q 为直线 CD 上一动点,且 AB 与 CD 的位置 关系保持不变,当点 Q 在射线 CD 上运动时(不与点 C 重合),∠PQD,∠APQ 与∠ BAC 有何数量关系?写出结论,并说明理由.

-
科目: 来源: 题型:
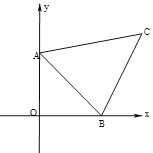
查看答案和解析>>【题目】如图,在平面直角坐标系中,A(0,3),B(3,0),C(5,4),∠OAB=∠OBA=45°,点P为坐标系中第一象限内一点(不与C重合),若△BAP≌△ABC,则点P坐标为_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:(1)△BDA≌△AEC;(2)DE=BD+CE.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校计划购买排球、篮球,已知购买1个排球与1个篮球的总费用为180元;3个排球与2个篮球的总费用为420元.
(1)求购买1个排球、1个篮球的费用分别是多少元?
(2)若该学校计划购买此类排球和篮球共60个,并且篮球的数量不超过排球数量的2倍.求至少需要购买多少个排球?并求出购买排球、篮球总费用的最大值?
相关试题

