Question

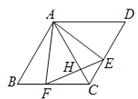
【题目】已知：菱形ABCD中，∠B＝60°，将含60°角的直角三角板的60°角的顶点放到菱形ABCD的顶点A处，两边分别与菱形的边BC，CD交于点F，E.

(1)(如图1)求证：AE=AF；

(2)连结EF，交AC于点H(如图2)，试探究AB，AF，AH之间的关系；

(3)若AB＝6，EF＝2，且CE＜DE，求FH的长.

Answer 1

【答案】(1)见解析；（2）见解析；（3）

【解析】分析：（1）由菱形的性质得到AD=AC， ∠ACB＝∠D，从而用ASA判定出△ACF≌△ADE．

（2）由AE＝AF，∠EAF=600，得到△AEF是等边三角形，进而得到∠BAF＝∠CAE，从而有△BAF∽△CAH，由相似三角形的性质即可得到结论．　

（3）由等边三角形的性质得到AF＝EF＝AE，再由AF2＝AB·AH，得到AH的长，进而得到CH的长，通过证明△CEH∽△DAE，得到，进而求出CE、EH，FH的长．

详解：（1）连结AC．

∵ABCD是菱形，∠B＝60°，

∴∠BAD＝∠BCD＝120°，∠D＝60°，

∠ACD＝∠ACB＝∠BCD，∠BAC＝∠DAC＝∠BAD．　

∴∠ACB＝∠DAC＝∠D＝60°．

∴AD＝AC．

∵∠EAF＝60°，∴∠CAF＋∠CAE＝∠DAE＋∠CAE．

∴∠CAF＝∠DAE．

∴△ACF≌△ADE．

∴AE＝AF．　

（2）∵AE＝AF，∠EAF=600，∴△AEF是等边三角形．

∴∠AEF＝600＝∠B．

∴∠BAF＋∠CAF＝∠CAE＋∠CAF＝600．　

∴∠BAF＝∠CAE．

∴△BAF∽△CAH．

∴．∴AB·AH＝AE·AF，即AF2＝AB·AH．　

（3）∵△AEF是等边三角形，∴AF＝EF＝AE．

∵AF2＝AB·AH，AB＝6，EF＝2，∴AH＝．　

∵∠B＝∠ACB＝600，∴AB＝AC＝6．　

∴CH＝AC－AH＝6－＝．

∵∠AEF＝600，∴∠CEH＋∠AED＝1200．

∵∠D＝600，∴∠DAE＋∠AED＝1200．

∴∠CEH＝∠DAE．

∵∠ACD＝∠D＝600，∴△CEH∽△DAE．　

∴．

∵四边形ABCD是菱形，∴AB＝BC＝CD＝AD＝6，　

∴．∴CE＝2或CE＝4．

∵CE＜DE，∴CE＝2．　

∴．∴EH＝．∴FH＝EF－EH＝．