Question

【题目】(8分)如图,△ABC中, ∠BAC=∠ADB,BE平分∠ABC交AD于点E,交AC于点F,过点E作EG//BC交AC于点G.(1)求证: AE=AF; (2)若AG=4，AC=7，求FG的长.

Answer 1

【答案】（1）见解析；（2）1.

【解析】分析：（1）由角平分线的定义和已知条件证出∠AFB=∠AEF，即可得出结论；（2）由SAS证明：△ABF≌△HBF，得出AF=FH，∠AFB=∠HFB，再证明1△AEG≌△FHC，得出AG=FC=4，即可得出结果．

本题解析：

（1）∵BF平分∠ABC

∴∠ABF=∠CBF

∵∠AFB=180°-∠ABF－∠BAF

∠BED=180°-∠CBF－∠ADB

又∵∠BAC=∠ADB

∴∠AFB=∠BED

∵∠AEF=∠BED

∴∠AFB=∠AEF

∴AE=AF

（2）如图，在BC上截取BH=AB，连接FH

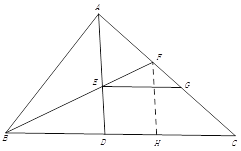
在△ABF和△HBF中

∵

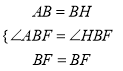
∴△ABF≌△HBF（SAS）

∴AF=FH，∠AFB=∠HFB

∵∠AFB=∠AEF

∴∠HFB=∠AEF

∴AE∥FH

∴∠GAE=∠CFH

∵EG∥BC

∴∠AGE=∠C

∵AE=AF

∴AE=FH

在△AEG和△FHC中

∵

∴△AEG≌△FHC（AAS）

∴AG=FC=4

∴FG=AG+ FC -AC=1