【题目】王勇和李华一起做风筝,选用细木棒做成如图所示的“筝形”框架,要求![]() ,
,![]() ,
,![]() .
.

(1)观察此图,是否是轴对称图形,若是,指出对称轴;
(2)![]() 和
和![]() 相等吗?为什么?
相等吗?为什么?
(3)判断![]() 是否被
是否被![]() 垂直平分,并说明你的理由.
垂直平分,并说明你的理由.
参考答案:
【答案】(1)是轴对称图形,对称轴是![]() 所在直线;(2)
所在直线;(2)![]() ;(3)
;(3)![]() 被
被![]() 垂直平分
垂直平分
【解析】
(1)是轴对称图形.对称轴是AC所在的直线.
(2)∠ABC=∠ADC.理由:△ABC△ADC(SSS),∴∠ABC=∠ADC.
(3)BD被AC垂直平分.理由多方面:比如B、D关于AC所在直线对称,∴BD被AC垂直平分;或者:BC=CD知△BCD是等腰三角形,又CA平分∠BCD,所以AC垂直平分BD;或者:证△BCO≌△DCO,∴BO=DO.又∠BOC=∠DOC,∴AC⊥BD.
解:(1)是轴对称图形,对称轴是![]() 所在直线
所在直线
(2)![]() ,理由:因为
,理由:因为![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,因此
,因此![]() .
.
(或者:因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,因此,
,因此,![]() )
)
(3)![]() 被
被![]() 垂直平分,理由:因为
垂直平分,理由:因为![]() ,所以,
,所以,![]() 是等腰三角形,由(2)知:
是等腰三角形,由(2)知:![]() ,可得
,可得![]() ,由等腰三角形的“三线合一”,所以
,由等腰三角形的“三线合一”,所以![]() 垂直平分
垂直平分![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:二次函数y=x2+bx+3的图象经过点(3,0).
(1)求b的值;
(2)求出该二次函数图象的顶点坐标和对称轴;
(3)在所给坐标系中画出二次函数y=x2+bx+3的图象.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 与
与 轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①当
轴交于点A(-1,0),顶点坐标为(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①当 时,
时,  ;②
;② ;③
;③ ;④
;④ 中,正确的是_______.
中,正确的是_______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系,△ABC的顶点都在格点上,请解答下列问题
(1)画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1,并写出点C1的坐标;
(2)画出将△ABC关于原点O对称的图形△A2B2C2,并写出点C2的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,延长
中,延长 至点
至点 ,使
,使 ,连接
,连接 ,作
,作 于点
于点 ,
, 交
交 的延长线于点
的延长线于点 ,且
,且 .
.
(1)求证:
 ;
;(2)如果
 ,求
,求 的度数.
的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家电销售商城电冰箱的销售价为每台2100元,空调的销售价为每台1750元,每台电冰箱的进价比每台空调的进价多400元,商城用80000元购进电冰箱的数量与用64000元购进空调的数量相等.
(1)求每台电冰箱与空调的进价分别是多少?
(2)现在商城准备一次购进这两种家电共100台,设购进电冰箱
 台,这100台家电的销售总利润为
台,这100台家电的销售总利润为 元,要求购进空调数量不超过电冰箱数量的2倍,试确定获利最大的方案以及最大利润.
元,要求购进空调数量不超过电冰箱数量的2倍,试确定获利最大的方案以及最大利润. -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现.
如图1,
 和
和 均为等边三角形,点
均为等边三角形,点 、
、 、
、 均在同一直线上,连接
均在同一直线上,连接 .
.
①求证:
 .
.②求
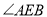 的度数.
的度数.③线段
 、
、 之间的数量关系为__________.
之间的数量关系为__________.(2)拓展探究.
如图2,
 和
和 均为等腰直角三角形,
均为等腰直角三角形, ,点
,点 、
、 、
、 在同一直线上,
在同一直线上, 为
为 中
中 边上的高,连接
边上的高,连接 .
.
①请判断
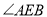 的度数为____________.
的度数为____________.②线段
 、
、 、
、 之间的数量关系为________.(直接写出结论,不需证明)
之间的数量关系为________.(直接写出结论,不需证明)
相关试题

