【题目】如图,菱形ABCD的边AB=8,∠B=60°,P是AB上一点,BP=3,Q是CD边上一动点,将梯形APQD沿直线PQ折叠,A的对应点A′.当CA′的长度最小时,CQ的长为( )
A.5
B.7
C.8
D.![]()
参考答案:
【答案】B
【解析】解:作CH⊥AB于H,如图,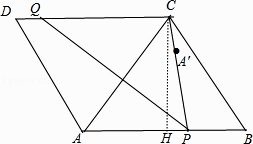
∵菱形ABCD的边AB=8,∠B=60°,
∴△ABC为等边三角形,
∴CH= ![]() AB=4
AB=4 ![]() ,AH=BH=4,
,AH=BH=4,
∵PB=3,
∴HP=1,
在Rt△CHP中,CP= ![]() =7,
=7,
∵梯形APQD沿直线PQ折叠,A的对应点A′,
∴点A′在以P点为圆心,PA为半径的弧上,
∴当点A′在PC上时,CA′的值最小,
∴∠APQ=∠CPQ,
而CD//AB,
∴∠APQ=∠CQP,
∴∠CQP=∠CPQ,
∴CQ=CP=7.
故选B.
作CH⊥AB于H,如图,根据菱形的性质可判断△ABC为等边三角形,则CH= ![]() AB=4
AB=4 ![]() ,AH=BH=4,再利用勾股定理计算出CP=7,再根据折叠的性质得点A′在以P点为圆心,PA为半径的弧上,利用点与圆的位置关系得到当点A′在PC上时,CA′的值最小,然后证明CQ=CP即可.
,AH=BH=4,再利用勾股定理计算出CP=7,再根据折叠的性质得点A′在以P点为圆心,PA为半径的弧上,利用点与圆的位置关系得到当点A′在PC上时,CA′的值最小,然后证明CQ=CP即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节约意识,我市出台阶梯电价计算方案:居民生活用电将月用电量分为三档,第一档为月用电量200度(含)以内,第二档为月用电量200~320度(含),第三档为月用电量320度以上.这三个档次的电价分别为:第一档0.52元/度,第二档0.57元/度,第三档0.82元/度.
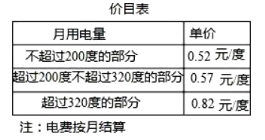
(1)若某户居民10月份电费78元,则该户居民10月份用电________度;
(2)若该户居民2月份用电340度,则应缴电费________元;
(3)用x(度)来表示月用电量,请根据x的不同取值范围,用含x的代数式表示出月用电费用.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)1点20分时,时钟的时针与分针的夹角是几度?
(2)在时钟上,7点到8点之间,时针和分针何时成30°的角?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点C(0,-2),直线l:y=kx-2k无论k取何值,直线总过定点B,
(1)求定点B的坐标.
(2)如图1,若点D为直线BC上(点(-1,-3)除外)一动点,过点D作x轴的垂线交y= - 3于点E,点F在直线BC上,距离D点为
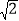 个单位,D点横坐标为t,ΔDEF的面积为S,求S与t函数关系式.
个单位,D点横坐标为t,ΔDEF的面积为S,求S与t函数关系式.(3)若直线BC关于x轴对称后再向上平移5个单位得到直线B1C1,如图2,点G(1,a)和H(6,b)是直线B1C1上两点,点P(m,n)为第一象限内(G、H两点除外)的一点,,且mn=6,直线PG和PH为分别交y轴于点MN两点,问线段OM、ON有什么数量关系,请证明.
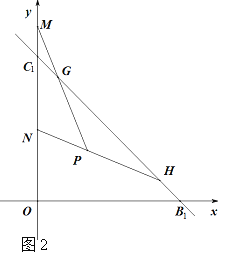
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四个均由十六个小正方形组成的正方形网格中,各有一个三角形ABC,那么这四个三角形中,不是直角三角形的是( )
A.
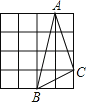 B.
B. 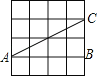 C.
C. 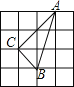 D.
D. 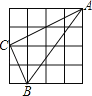
-
科目: 来源: 题型:
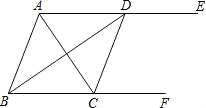
查看答案和解析>>【题目】如图,AE∥BF,AC平分∠BAE,交BF于点C,BD平分∠ABC,交AE于点D,连接CD.
(1)求证:四边形ABCD是菱形;
(2)若AB=5,AC=6,求AE,BF之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,长方形OABC的边OA在数轴上,O为原点,长方形OABC的面积为12,OC边长为3.

(1)数轴上点A表示的数为________.
(2)将长方形OABC沿数轴水平移动,移动后的长方形记为O′A′B′C′,移动后的长方形O′A′B′C′与原长方形OABC重叠部分(如图2中阴影部分)的面积记为S.
①当S恰好等于原长方形OABC面积的一半时,数轴上点A′表示的数是多少?
②设点A的移动距离AA′=x.
(ⅰ)当S=4时,求x的值;
(ⅱ)D为线段AA′的中点,点E在线段OO′上,且OE=
 OO′,当点D,E所表示的数互为相反数时,求x的值.
OO′,当点D,E所表示的数互为相反数时,求x的值.
相关试题

