【题目】如图,在Rt△ABC中,∠A=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,则EF的最小值为( )

A.2B.2.2C.2.4D.2.5
参考答案:
【答案】C
【解析】
根据已知得出四边形AEPF是矩形,得出EF=AP,要使EF最小,只要AP最小即可,根据垂线段最短得出即可.
解:连接AP,
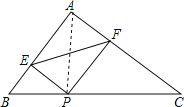
∵∠A=90°,PE⊥AB,PF⊥AC,
∴∠A=∠AEP=∠AFP=90°,
∴四边形AFPE是矩形,
∴EF=AP,
要使EF最小,只要AP最小即可,
过A作AP⊥BC于P,此时AP最小,
在Rt△BAC中,∠A=90°,AC=4,AB=3,由勾股定理得:BC=5,
由三角形面积公式得:![]() ,
,
∴AP=2.4,
即EF=2.4,
故选:C.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,反比例函数y=
 的图象与一次函数y=x+b的图象交
的图象与一次函数y=x+b的图象交于点A(1,4)、点B(-4,n).

(1)求一次函数和反比例函数的解析式;
(2)求△OAB的面积;
(3)直接写出一次函数值大于反比例函数值的自变量x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形
 中,点
中,点 在边
在边 上(点
上(点 与点
与点 、
、 不重合),过点
不重合),过点 作
作 ,
, 与边
与边 相交于点
相交于点 ,与边
,与边 的延长线相交于点
的延长线相交于点 .
.(1)
 与
与 有什么样的数量关系?请直接写出你的结论:____________________
有什么样的数量关系?请直接写出你的结论:____________________(2)
 、
、 、
、 的数量之间具有怎样的关系?并证明你所得到的结论.
的数量之间具有怎样的关系?并证明你所得到的结论.(3)如果正方形的边长是1,
 ,直接写出点
,直接写出点 到直线
到直线 的距离.
的距离.
解:(1)
 与
与 的数量关系:____________________
的数量关系:____________________ (2)
 、
、 、
、 的数量之间的关系是 .
的数量之间的关系是 .证明:
(3)点
 到直线
到直线 的距离是 .
的距离是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
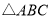 中,
中, ,
,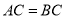 ,
,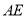 是
是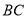 边上的中线,过
边上的中线,过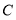 作
作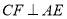 ,垂足为
,垂足为 ,过
,过 作
作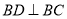 交
交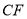 的延长线于
的延长线于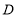 ,则下列结论正确的是______.(请填写序号)
,则下列结论正确的是______.(请填写序号)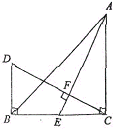
①若
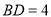 ,则
,则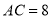 ;②
;②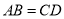 ;③
;③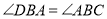 ;④
;④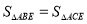 ;⑤
;⑤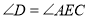 ;⑥连接
;⑥连接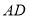 ,则
,则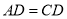 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同;
④甲队比乙队提前2天完成任务.

A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】①甲队每天挖
 =100米,正确.
=100米,正确.②乙队开挖两天后,每天挖;
 米,正确.
米,正确.③当x=4时,甲、乙两队交点在x=4处,所以挖管道长度相同.正确.
④由②知,甲挖完的时候,乙还有100米,100
 2. 甲队比乙队提前2天完成任务.正确.
2. 甲队比乙队提前2天完成任务.正确.故选D.
【题型】单选题
【结束】
11【题目】103 000用科学记数法表示为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设立了一个如图可以自由转动的转盘,并规定:顾客每购买300元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红、绿或黄色区域,顾客就可以获得100元、50元,20元的购物券.(转盘被等分成20个扇形),已知甲顾客购物320元.

(1)他获得购物券的概率是多少?
(2)他得到100元、50元、20元购物券的概率分别是多少?
(3)若要让获得20元购物券的概率变为
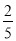 ,则转盘的颜色部分怎样修改?请说明理由.
,则转盘的颜色部分怎样修改?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AD是中线,∠BAD=∠B+∠C,tan∠ABC=
 ,则tan∠BAD=________.
,则tan∠BAD=________.
【答案】

【解析】延长AD到E,使AD=DE,CF
 ,
,在
 与
与 ,
,,
 ,所以
,所以 ,
,
 是等腰三角形,s
是等腰三角形,s设EM= x,DE=11,MC=10,
 ,
, ,
, x=
x= ,
, tan∠BAD=
tan∠BAD= .
.故答案为
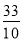 .
.
点睛:倍长中线法构造全等三角形,如图,AD是中线,令AD=DE,则
 ADC全等
ADC全等 EBD.
EBD.
【题型】填空题
【结束】
21【题目】先化简,再求值:
 ÷(
÷( -a+2),其中a=2sin60°+3tan45°.
-a+2),其中a=2sin60°+3tan45°.
相关试题

