搜索
【题目】按图示方法用小棒摆正六边形，摆15个正六边形需要（__________）根小棒；摆n个正六边形需要（__________）根小棒.
参考答案：
【答案】76 5n＋1．
【解析】
摆1个六边形需要6根小棒，可以写作：5×1＋1；摆2个需要11根小棒，可以写作：5×2＋1；摆3个需要16根小棒，可以写成：5×3＋1；…由此可以推理得出一般规律解答问题．
解：当n＝1时，需要小棒1×5＋1＝6（根），
当n＝2时，需要小棒2×5＋1＝11（根），
当n＝3时，需要小棒3×5＋1＝16（根），
当n＝4时，需要小棒4×5＋1＝21（根），
…
当n＝15时，需要小棒15×5＋1＝76（根）
摆n个六边形需要：5n＋1根小棒．
∴摆15个正六边形需要76根小棒；摆n个六边形需要5n＋1根小棒．
故答案为：76；5n＋1．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点A是反比例函数y＝
（m＜0）位于第二象限的图像上的一个动点，过点A作AC⊥x轴于点C；M为是线段AC的中点，过点M作AC的垂线，与反比例函数的图像及y轴分别交于B、
D两点．顺次连接A、B、C、D．设点A的横坐标为n．
（1）求点B的坐标（用含有m、n的代数式表示）；
（2）求证：四边形ABCD是菱形；
（3）若△ABM的面积为2，当四边形ABCD是正方形时，求直线AB的函数表达式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，已知直线y=x+3与x轴交于点A，与y轴交于点B，将直线在x轴下方的部分沿x轴翻折，得到一个新函数的图象（图中的“V形折线”）．
（1）类比研究函数图象的方法，请列举新函数的两条性质，并求新函数的解析式；
（2）如图2，双曲线y=
与新函数的图象交于点C（1，a），点D是线段AC上一动点（不包括端点），过点D作x轴的平行线，与新函数图象交于另一点E，与双曲线交于点P．①试求△PAD的面积的最大值；
②探索：在点D运动的过程中，四边形PAEC能否为平行四边形？若能，求出此时点D的坐标；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠ACB＝90°，sinA＝
，BC＝8，点D是AB的中点，过点B作CD的垂线，垂足为点E.(1)求线段CD的长；
(2)求cos∠ABE的值。
-
科目： 来源： 题型：
查看答案和解析>>【题目】直接写得数.
1÷0.005= 7.8+3.02= 0.5×0.02= 75%-0.69= 0.023=
+0.025= 
÷0.0625= 
= 1.2-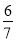
×0= 102×41≈ -
科目： 来源： 题型：
查看答案和解析>>【题目】反比例函数y=
(k≠0)与一次函数y=－x+5的一个交点是A(1,n).(1)求反比例函数y=
(k≠0)的表达式；(2)当一次函数的函数值大于反比例函数的函数值时，直接写出自变量x的取值范围为 。
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，等边△ABC沿射线BC向右平移到△DCE的位置，连接AD、BD，则下列结论：①AD=BC；②BD、AC互相平分；③四边形ACED是菱形．其中正确的个数是
A. 0 B. 1 C. 2 D. 3
相关试题
