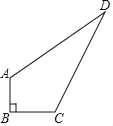
【题目】某中学有一块四边形的空地ABCD,如图所示,学校计划在空地上种植草皮,经测量∠B=90°,AB=3m,BC=4m,CD=12m,AD=13m.若每平方米草皮需要200元,问学校需要投入多少资金买草皮?
参考答案:
【答案】学校需要投入7200元买草皮.
【解析】
直接利用勾股定理的逆定理得出∠ACD=90°,再利用直角三角形的性质得出答案.
连接AC
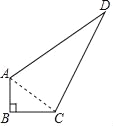
∵∠B=90°,AB=3m,BC=4m,BC=12m,
AC2=AB2+AD2=32+42=25,AC=5m,
∴AC2+CD2=25+144=169=132
又∵AD2=132,
∴AC2+CD2=CD2
∴∠ACD=90°,
∴△ACD是直角三角形,
∴四边形ABCD的面积=6+30=36(m2),
∴学校要投入资金为:200×36=7200(元);
答:学校需要投入7200元买草皮.
-
科目: 来源: 题型:
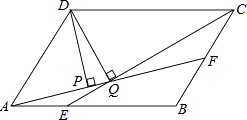
查看答案和解析>>【题目】如图,平行四边形ABCD中,AB:BC=3:2,∠DAB=60°,E在AB上,且AE:EB=1:2,F是BC的中点,过D分别作DP⊥AF于P,DQ⊥CE于Q,则DP:DQ等于( )
A.3:4
B. :2
:2 
C. :2
:2 
D.2 :
: 
-
科目: 来源: 题型:
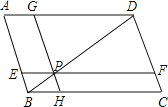
查看答案和解析>>【题目】在ABCD中,EF∥BC,GH∥AB,EF、GH的交点P在对角线BD上,图中面积相等的平行四边形有( )对.
A. 0 B. 1 C. 2 D. 3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论::①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的结论的个数有( )

A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
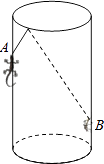
查看答案和解析>>【题目】如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,则壁虎捕捉蚊子的最短距离为 m(容器厚度忽略不计).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知直线l:y=
 x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M8坐标为 .
x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1 , 过点N1作直线l的垂线交x轴于点M2 , …;按此作法继续下去,则点M8坐标为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】相传有个人不讲究说话艺术常引起误会,一天他设宴请客,他看到几个人没来,就自言自语:“怎么该来的还不来呢?”客人听了,心想难道我们是不该来的,于是已到的客人的一半走了,他一看十分着急,又说:“嗨,不该走的倒走了!”剩下的人一听,是我们该走啊!又有剩余客人的三分之一离开了,他着急地一拍大腿:“我说的不是他们.”于是剩下的6个人也走了,聪明的你知道最开始来了多少客人吗?( )
A. 16B. 18C. 20D. 22
相关试题

