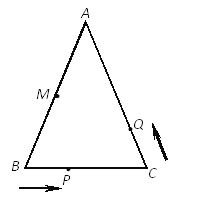
【题目】如图，已知△ABC中，AB=AC=12厘米，（即∠B=∠C），BC=9厘米，点M为AB的中点，

（1）如果点P在线段BC上以2厘米/秒的速度由点B向点C运动，同时，点Q在线段CA上由点C向点A运动.

①若点Q的运动速度与点P的运动速度相等，经过1.5秒后，△BPM与△CQP是否全等？请说明理由.

②若点Q的运动速度与点P的运动速度不相等，当点Q的运动速度为多少时，能够使△BPM与△CQP全等？

（2）若点Q以②中的运动速度从点C出发，点P以原来的运动速度从点B同时出发，都逆时针沿△ABC三边运动，求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇？

参考答案：

【答案】（1）见解析；（2）能，①vQ=cm/s；②经过36s第一次相遇，相遇点在边BC上

【解析】分析：(1)、①先求得BP=CQ=3，PC=BM=6，然后根据等边对等角求得∠B=∠C，最后根据SAS即可证明；②因为VP≠VQ，所以BP≠CQ，又∠B=∠C，要使△BPD与△CQP全等，只能BP=CP=4.5，根据全等得出CQ=BM=6，然后根据运动速度求得运动时间，根据时间和CQ的长即可求得Q的运动速度；(2)、因为VQ＞VP，只能是点Q追上点P，即点Q比点P多走AB+AC的路程，据此列出方程，解这个方程即可求得．

详解：（1）①∵t=1.5s， ∴BP=CQ=2×1.5=3， ∴CP=BC—BP=6，∵BM= AB=6， ∴BM=CP

又∵BP=CQ，∠B=∠C， ∴△MBP≌△PCQ

②能， ∵vP≠vQ，∴BP≠CQ，∵∠B=∠C，∴若△BMP≌△CQP，

则CQ=BM=6，CP=BP= BC=4.5， ∴此时得时间t= = s ， ∴vQ= == cm/s

(2)、设经过x秒后两点第一次相遇.

由题意得：x= 2x + 2×12， 解得：x=36(s)， 此时点P共运动了 2×36=72 cm，

∵72=2×33+6， ∴在BC边相遇.

答：经过36s第一次相遇，相遇点在边BC上

关闭