【题目】某校学生会决定从三名学生会干事中选拔一名干事,对甲、乙、丙三名候选人进行了笔试和面试,三人的测试成绩如下表所示:
测试项目 | 测试成绩/分 | ||
甲 | 乙 | 丙 | |
笔试 | 75 | 80 | 90 |
面试 | 93 | 70 | 68 |
根据录用程序,学校组织200名学生采用投票推荐的方式,对三人进行民主测评,三人得票率(没有弃权,每位同学只能推荐1人)如扇形统计图所示,每得一票记1分.
(1)扇形统计图中![]() = , 分别计算三人民主评议的得分;
= , 分别计算三人民主评议的得分;
(2)根据实际需要,学校将笔试、面试、民主评议三项得分按4:3:3的比例确定个人成绩,得分最高者将被选中,通过计算说明三人中谁被选中?

参考答案:
【答案】(1)a=25;甲民主评议的得分50(分);乙民主评议的得分是80(分);丙民主评议的得分是: 70(分)(2)丙会被选中.
【解析】试题分析:(1)用1-40%-35%即可得到a的值,再分别用200乘以三人的得票率,求出三人民主评议的得分各是多少即可;
(2)根据加权平均数的计算方法列式计算,分别求出三人的得分各是多少;然后比较大小,判断出三人中谁的得分最高即可.
试题解析:(1)a%=1-40%-35%,所以a=25,
甲民主评议的得分是:200×25%=50(分);
乙民主评议的得分是:200×40%=80(分);
丙民主评议的得分是:200×35%=70(分);
(2)甲的成绩是:(75×4+93×3+50×3)÷(4+3+3)=729÷10=72.9(分),
乙的成绩是:(80×4+70×3+80×3)÷(4+3+3)=770÷10=77(分),
丙的成绩是:(90×4+68×3+70×3)÷(4+3+3)=774÷10=77.4(分),
∵77.4>77>72.9,∴丙的得分最高,将被选中.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意结合图形填空:如图,

点
 在
在 上,点
上,点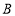 在
在 上,
上, ,
,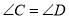 .试说明:
.试说明: ∥
∥ .将过程补充完整.
.将过程补充完整.解:∵
 (已知)
(已知)且
 ( )
( )∴
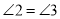 (等量代换)
(等量代换)∴ ∥ ( )
∴
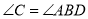 ( )
( )又∵
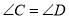 (已知)
(已知)∴ = (等量代换 )
∴
 ∥
∥ ( )
( ) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
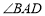 ,点
,点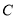 是
是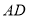 边上的一点,按要求画图,并保留作图痕迹.
边上的一点,按要求画图,并保留作图痕迹.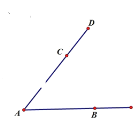
(1)用尺规作图法在
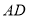 的右侧以点
的右侧以点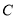 为顶点作
为顶点作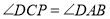 ;
;(2)射线
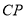 与
与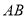 的位置关系是____________,理由是____________.
的位置关系是____________,理由是____________.(3)画出表示点
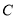 到
到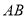 的距离的线段和表示点
的距离的线段和表示点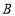 到
到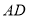 的距离的线段.
的距离的线段. -
科目: 来源: 题型:
查看答案和解析>>【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.
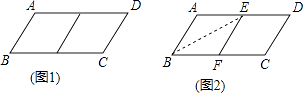
(1)猜想与计算:
邻边长分别为3和5的平行四边形是阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD是阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,等边△ABC为⊙O的内接三角形,点G和点F在⊙O上且位于点A的两侧,连接BF、CG交于点E,且BF=CG.
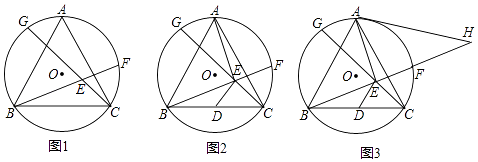
(1)求证:∠BEC=120°;
(2)如图2,取BC边中点D,连接AE、DE,求证:AE=2DE;
(3)如图3,在(2)的条件下,过点A作⊙O的切线交BF的延长线于点H,若AE=AH=4,请求出⊙O的半径长. -
科目: 来源: 题型:
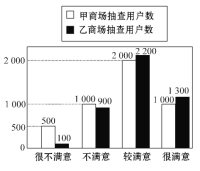
查看答案和解析>>【题目】在“3·15”消费者权益日的活动中,对甲、乙两家商场售后服务的满意度进行了抽查.如图反映了被抽查用户对两家商场售后服务的满意程度(以下称:用户满意度),分为很不满意、不满意、较满意、很满意四个等级,并依次记为1分、2分、3分、4分.
(1)分别求出甲、乙两商场的用户满意度分数的平均值(计算结果精确到0.01).
(2)请你根据所学的统计知识,判断哪家商场的用户满意度较高,并简要说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,点C是线段AB上的一点,点D是线段AB的中点,点E是线段BC的中点.
(1)当AC=8,BC=6时,求线段DE的长度;
(2)当AC=m,BC=n(m>n)时,求线段DE的长度;
(3)从(1)(2)的结果中,你发现了什么规律?请直接写出来.
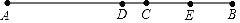
相关试题

