【题目】如图,直线y1=x+2与双曲线 ![]() 相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.
相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.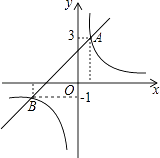
(1)求k的值;
(2)若y1<y2 , 请你根据图象确定x的取值范围.
参考答案:
【答案】
(1)解:把y=3代入y1=x+2得x=1,
把y=﹣1代入y1=x+2得x=﹣3,
∴A(1,3),B(﹣3,﹣1),
把A(1,3)代入 ![]() 得k=3
得k=3
(2)解:由图象知:当x<﹣3,或0<x<1时,y1<y2,
即若y1<y2,x的取值范围为:x<﹣3,或0<x<1
【解析】(1)由A、B在直线y1=x+2上,可求出A、B两点的坐标,再由待定系数法可求出反比例函数的解析式;
(2)结合图像可直接写出.
【考点精析】解答此题的关键在于理解确定一次函数的表达式的相关知识,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法.
-
科目: 来源: 题型:
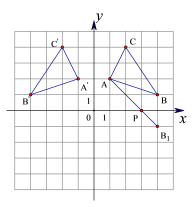
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标为A(1,2),B(4,1),C(2,4).
(1)在图中画出△ABC关于y轴对称的图形△A’B’C’;
(2)在图中x轴上作出一点P,使PA+PB的值最小;并写出点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(1)求∠AON的度数.
(2)写出∠DON的余角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.

(1)求证:△ACD∽△ABC;
(2)若AD=6,AB=10,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭
 出发,晚上停留在
出发,晚上停留在 处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):+5,-8,+10,-12,+6,-18,+5,-2.
(1)
 处在岗亭
处在岗亭 的什么方向?距离岗亭
的什么方向?距离岗亭 多远?
多远?(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
-
科目: 来源: 题型:
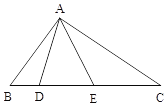
查看答案和解析>>【题目】已知:如图,在△ABC中,点D,E是边BC上的两点,且AB=BE,AC=CD.
(1)若∠BAC =90°,求∠DAE的度数;
(2)若∠BAC=120°,直接写出∠DAE的度数
(3)设∠BAC=α,∠DAE=β,猜想α与β的之间数量关系(不需证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 、
、 两点在线段
两点在线段 上,且
上,且 ,点
,点 为
为 的中点.
的中点.
(1)判断线段
 与
与 的大小关系,并说明理由;
的大小关系,并说明理由;(2)若
 ,求
,求 的长.
的长.
相关试题

