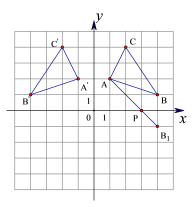
【题目】如图,在平面直角坐标系中,△ABC三个顶点的坐标为A(1,2),B(4,1),C(2,4).
(1)在图中画出△ABC关于y轴对称的图形△A’B’C’;
(2)在图中x轴上作出一点P,使PA+PB的值最小;并写出点P的坐标.
参考答案:
【答案】(1)如图所示见解析;(2)如图所示见解析, 点P的坐标为(3,0).
【解析】
(1)根据关于y轴对称的点的坐标特征分别作出点A、B、C关于y轴的对称点A’,B’,C’,即可得到△A’B’C’;
(2)将B点关于x轴对称得到B1,再连接AB1与x轴的交点就是P点.
(1)如图所示;
(2)如图所示;
点P的坐标为(3,0)
点B和B1关于x轴对称,连结AB1交x轴于P,则PB=PB1,
此时PA+PB1的值最小,
设直线AB1的解析式为y=kx+b,
把B1(4,-1),A(1,2)代入y=kx+b,,
解得k=-1,b=3.
所以直线AB1的解析式为y=x+3,
当y=0时, x+3=0,解得x=3,
所以点P的坐标为(3,0).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点N(0,6),点M在x轴负半轴上,ON=3OM.A为线段MN上一点,AB⊥x轴,垂足为点B,AC⊥y轴,垂足为点C.
(1)写出点M的坐标;
(2)求直线MN的表达式;
(3)若点A的横坐标为-1,求矩形ABOC的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在我市中小学生“我的中国梦”读书活动中,某校对部分学生做了一次主题为“我最喜爱的图书”的调查活动,将图书分为甲、乙、丙、丁四类,学生可根据自己的爱好任选其中一类.学校根据调查情况进行了统计,并绘制了不完整的条形统计图和扇形统计图.

请你结合图中信息,解答下列问题:
(1)本次共调查了 名学生;
(2)被调查的学生中,最喜爱丁类图书的有 人,最喜爱甲类图书的人数占本次被调查人数的 %;
(3)在最喜爱丙类学生的图书的学生中,女生人数是男生人数的1.5倍,若这所学校共有学生1500人,请你估计该校最喜爱丙类图书的女生和男生分别有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,△ABC是直角三角形,∠ACB=90°,点D、E分别在AB、BC上,且CA=CD=CE,下列说法: ①∠EDB=45° ②∠EAD=
 ∠ECD ③当△CDB是等腰三角形时,△CAD是等边三角形④当∠B=22.5°时,△ACD≌△DCE .其中正确的个数有( )
∠ECD ③当△CDB是等腰三角形时,△CAD是等边三角形④当∠B=22.5°时,△ACD≌△DCE .其中正确的个数有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知直线AB和CD相交于点O,OM平分∠BOD,∠MON=90°,∠AOC=50°.
(1)求∠AON的度数.
(2)写出∠DON的余角.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.

(1)求证:△ACD∽△ABC;
(2)若AD=6,AB=10,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y1=x+2与双曲线
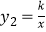 相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.
相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.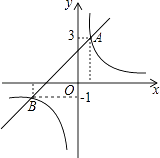
(1)求k的值;
(2)若y1<y2 , 请你根据图象确定x的取值范围.
相关试题

