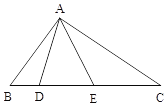
【题目】已知:如图,在△ABC中,点D,E是边BC上的两点,且AB=BE,AC=CD.
(1)若∠BAC =90°,求∠DAE的度数;
(2)若∠BAC=120°,直接写出∠DAE的度数
(3)设∠BAC=α,∠DAE=β,猜想α与β的之间数量关系(不需证明).
参考答案:
【答案】(1)45°;(2)∠DAE=30°;(3)α+2β=180.
【解析】
(1)由题意得出∠BEA=![]() ,∠CDA =
,∠CDA =![]() ,再在△ADE中
,再在△ADE中
利用内角和等于180°即可.
(2)同(1)理可快速得出答案.
(3)综合(1)(2)可总结出α与β的之间数量关系.
(1)∵AB=BE ,AC=CD
∴∠BEA=![]() ,∠CDA =
,∠CDA =![]()
在△ADE中
∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )=
(180°∠BAC )=![]() ×(180°90°)=45°
×(180°90°)=45°
(2)∠DAE=30°
理由:∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )= 30°
(180°∠BAC )= 30°
(3)α+2β=180
理由:∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )
(180°∠BAC )
∠DAE=![]() (180°∠BAC )
(180°∠BAC )
α+2β=180.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是AB上一点,连接CD,且∠ACD=∠ABC.

(1)求证:△ACD∽△ABC;
(2)若AD=6,AB=10,求AC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y1=x+2与双曲线
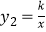 相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.
相交于A,B两点其中点A的纵坐标为3,点B的纵坐标为﹣1.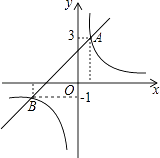
(1)求k的值;
(2)若y1<y2 , 请你根据图象确定x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】一天,某交警巡逻车在东西方向的青年路上巡逻,他从岗亭
 出发,晚上停留在
出发,晚上停留在 处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):
处.规定向东方向为正,向西方向为负,当天行驶情况记录如下(单位:千米):+5,-8,+10,-12,+6,-18,+5,-2.
(1)
 处在岗亭
处在岗亭 的什么方向?距离岗亭
的什么方向?距离岗亭 多远?
多远?(2)若巡逻车每行驶1千米耗油0.1升,这一天共耗油多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 、
、 两点在线段
两点在线段 上,且
上,且 ,点
,点 为
为 的中点.
的中点.
(1)判断线段
 与
与 的大小关系,并说明理由;
的大小关系,并说明理由;(2)若
 ,求
,求 的长.
的长. -
科目: 来源: 题型:
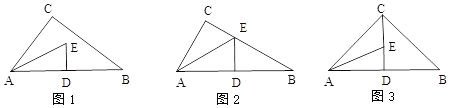
查看答案和解析>>【题目】如图1,△ABC是直角三角形,∠C=90°,∠CAB的角平分线AE与 AB的垂直平分线DE相交于点E.
(1)如图2,若点E正好落在边BC上.
①求∠B的度数
②证明:BC=3DE
(2)如图3,若点E满足C、E、D共线.
求证:AD+DE=BC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小丽两位同学学习数学都养成了良好的预习习惯.某天他俩预习了课本第107页上的问题3,题目如下:
某小组计划做一批“中国结”,如果每人做5个,那么比计划多了9个;如果每人做4个,那么比计划少15个.该小组共有多少人?计划做多少个“中国结”?
他俩都没有看课本上的解答过程,而是独立思考,分别列出了如下尚不完整的方程:
小明:
 ; 小丽:
; 小丽: .
.(1)在小明、小丽所列的方程中,“□”中是运算符号,“( )”中是数字,试分别指出未知数
 、
、 表示的意义;
表示的意义;(2)试选择一种方法,将问题3解答完整.
相关试题

