【题目】如图,已知△EFG≌△NMH, ∠F与∠M是对应角.
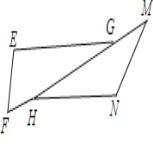
(1)写出相等的线段与相等的角;
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.
参考答案:
【答案】(1)EF=NM,EG=NH,FG=MH,∠F=∠M, ∠E=∠N, ∠EGF=∠NHM (2)MN=2.1cm,HG=2.2cm.
【解析】
试题分析:(1)因为△EFG≌△NMH,故有全等三角形的对应边和对应角相等. (2)因为△EFG≌△NMH,故EF=NM,![]() ,即可求出各自的长度.
,即可求出各自的长度.
试题解析:(1)![]() △EFG≌△NMH,∠F与∠M是对应角
△EFG≌△NMH,∠F与∠M是对应角 ![]() 在△EFG和△NMH中,有EF=NM,EG=NH,FG=MH
在△EFG和△NMH中,有EF=NM,EG=NH,FG=MH
∠F=∠M, ∠E=∠N, ∠EGF=∠NHM ;(2)∵由(1)可知,EF=NM,EF=2.1cm ∴MN=2.1 又![]() MH=FG=3.3 FH=1.1 ∴
MH=FG=3.3 FH=1.1 ∴![]() =3.3-1.1=2.2cm.
=3.3-1.1=2.2cm.
考点:全等三角形的性质.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将长方形ABCD沿着对角线BD折叠,使点C落在
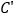 处,
处,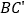 交AD于点E.
交AD于点E.(1)试判断△BDE的形状,并说明理由;
(2)若AB=6,
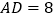 ,求△BDE的面积.
,求△BDE的面积.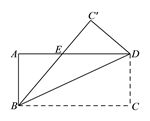
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′,则补充的这个条件是( )

A. BC=B′C′ B. ∠A=∠A′ C. AC=A′C′ D. ∠C=∠C′
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校学生利用双休时间去距学校10km的炎帝故里参观,一部分学生骑自行车先走,过了20min后,其余学生乘汽车沿相同路线出发,结果他们同时到达.已知汽车的速度是骑车学生速度的2倍,求骑车学生的速度和汽车的速度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图形中,既是轴对称图形又是中心对称图形的是( )
A.等腰三角形B.直角三角形C.平行四边形D.菱形
-
科目: 来源: 题型:
查看答案和解析>>【题目】一幅长20cm、宽12cm的图案,如图,其中有一横两竖的彩条,横、竖彩条的宽度比为3:2.设竖彩条的宽度为xcm,图案中三条彩条所占面积为ycm2.
(1)求y与x之间的函数关系式;
(2)若图案中三条彩条所占面积是图案面积的
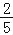 ,求横、竖彩条的宽度.
,求横、竖彩条的宽度.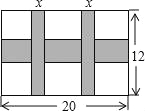
-
科目: 来源: 题型:
查看答案和解析>>【题目】要使一个平行四边形成为正方形,则需添加的条件为____________(填上一个正确的结论即可).
相关试题

