搜索
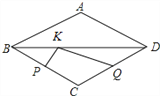
【题目】如图，点P、Q是边长为2的菱形ABCD中两边BC和CD的中点，K是BD上一动点，则KP+KQ的最小值为________．
参考答案：
【答案】2
【解析】分析：先作点P关于BD的对称点P′，连接P′Q交BD于K，此时PK+QK有最小值．然后证明四边形BCQP′为平行四边形，即可求出PK+QK=P′Q=BC=2．
详解：
作点P关于BD的对称点P′，连接P′Q交BD于K，此时KP+KQ有最小值，最小值为P′Q的长．
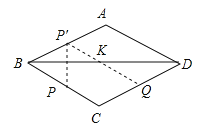
∵菱形ABCD关于BD对称，P是BC边上的中点，
∴P′是AB的中点，
又∵Q是CD边上的中点，
∴BP′∥CQ，BP′=CQ，
∴四边形BCQP′是平行四边形，
∴P′Q=BC=2，
∴PK+KQ=P′Q=2，即KP+KQ的最小值为2，
故答案为：2．
-
科目： 来源： 题型：
查看答案和解析>>【题目】对于两个已知图形G1、G2，在G1上任取一点P，在G2上任取一点Q，当线段PQ的长度最小时，我们称这个最小长度为G1、G2的“密距”.例如，如上图，
，
，
，则点A与射线OC之间的“密距”为
，点B与射线OC之间的“密距”为3，如果直线y＝x-1和双曲线
之间的“密距”为
，则k值为（ ）
A. k=4 B. k=－4 C. k=6 D. k=－6
-
科目： 来源： 题型：
查看答案和解析>>【题目】为了解学生课余活动情况，某校对参加绘画、书法、舞蹈、乐器这四个课外兴趣小组的人员分布情况进行抽样调查，并根据收集的数据绘制了下面两幅不完整的统计图，请根据图中提供的信息，解答下面的问题：
（1）此次共调查了多少名同学？
（2）将条形图补充完整，并计算扇形统计图中书法部分的圆心角的度数；
（3）如果该校共有1000名学生参加这4个课外兴趣小组，而每个教师最多只能辅导本组的20名学生，估计每个兴趣小组至少需要准备多少名教师？
-
科目： 来源： 题型：
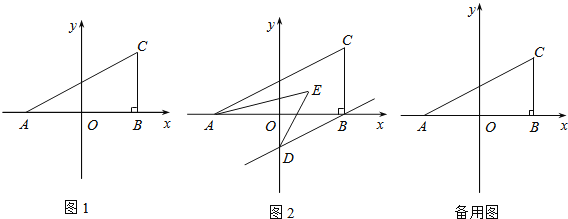
查看答案和解析>>【题目】如图1，在平面直角坐标系中，A（a，0），C（b，2），且满足
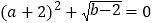，过C作CB⊥x轴于B，（1）求a，b的值；
（2）在y轴上是否存在点P，使得△ABC和△OCP的面积相等，求出P点坐标；
（3）若过B作BD∥AC交y轴于D，且AE，DE分别平分∠CAB，∠ODB，如图2，
①求：∠CAB＋∠ODB的度数；
②求：∠AED的度数.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．
（1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．
（2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？
-
科目： 来源： 题型：
查看答案和解析>>【题目】解下列方程
；
；
；
如果方程
与方程
的解相同，求
的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，边长为a的正方形发生形变后成为边长为a的菱形，如果这个菱形的一组对边之间的距离为h，我们把
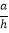的值叫做这个菱形的“形变度”；例如，当形变后的菱形是如图2形状（被对角线BD分成2个等边三角形），则这个菱形的“形变度”为2：
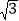；如图3，正方形由16个边长为1的小正方形组成，形变后成为菱形，△AEF（A、E、F是格点）同时形变为△A'E'F'，若这个菱形的“形变度”k=
，则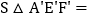
_______；
相关试题
