搜索
【题目】如图，EF为△ABC的中位线，△AEF的面积为6，则四边形EBCF的面积为 ． 
参考答案：
【答案】18
【解析】解：∵E、F分别是AB，AC的中点，
∴EF∥BC，
∴△AEF∽△ABC，
∴ 
=（ 
）2= 
，
∵△AEF的面积为6，
∴△ABC的面积是24，
∴四边形EBCF的面积是24﹣6=18，
所以答案是：18．
【考点精析】根据题目的已知条件，利用三角形中位线定理和相似三角形的判定与性质的相关知识可以得到问题的答案，需要掌握连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某课题组为了解全市七年级学生对数学知识的掌握情况，在一次数学检测中，从全市2000名年级考生中随机抽取部分学生的数学成绩进行调查，并将调查结果绘制成如下图表：
（1）表中
和
所表示的数分别为：
，
；（2）请在图中补全频数分布直方图；
（3）如果把成绩在100分以上（含100分）定为优秀，那么该市2000名七年级考生数学成绩为优秀的学生约有多少名？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，矩形ABCD中，AD=
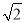，F是DA延长线上一点，G是CF上一点，且∠ACG=∠AGC，∠GAF=∠F=20°，则AB= ．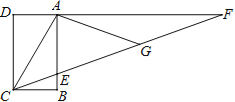
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形
的边长为
， 
、
、
分别是
、
、
上的动点，且
．（
）求证：四边形
是正方形．（
）判断直线
是否经过某一定点，说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】据调查，超速行驶是引发交通事故的主要原因之一，所以规定以下情境中的速度不得超过15m/s，在一条笔直公路BD的上方A处有一探测仪．如图，AD=24m，∠D=90°，第一次探测到一辆轿车从B点匀速向D点行驶，测得∠ABD=31°，2秒后到达C点，测得∠ACD=50°
（1）求B，C的距离．
（2）通过计算，判断此轿车是否超速．（tan31°≈0.6，tan50°≈1.2，结果精确到1m） -
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，已知平行四边形ABCD，对角线AC，BD相交于点O，∠OBC=∠OCB．
（1）求证：平行四边形ABCD是矩形；
（2）请添加一个条件使矩形ABCD为正方形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】学校准备购进一批节能灯，已知1只A型节能灯和3只B型节能灯共需26元；3只A型节能灯和2只B型节能灯共需29元．
（1）求一只A型节能灯和一只B型节能灯的售价各是多少元；
（2）学校准备购进这两种型号的节能灯共50只，并且A型节能灯的数量不多于B型节能灯数量的3倍，请设计出最省钱的购买方案，并说明理由．
相关试题
