【题目】如图,正方形![]() 的边长为
的边长为![]() ,
, ![]() 、
、![]() 、
、![]() 分别是
分别是![]() 、
、![]() 、
、![]() 上的动点,且
上的动点,且![]() .
.
(![]() )求证:四边形
)求证:四边形![]() 是正方形.
是正方形.
(![]() )判断直线
)判断直线![]() 是否经过某一定点,说明理由.
是否经过某一定点,说明理由.

参考答案:
【答案】(1)证明见解析;(2)![]() 必过
必过![]() 中点这个点,理由见解析.
中点这个点,理由见解析.
【解析】试题分析:(1)由正方形的性质得出∠A=∠B=∠C=∠D=90°,AB=BC=CD=DA,证出AH=BE=CF=DG,由SAS证明△AEH≌△BFE≌△CGF≌△DHG,得出EH=FE=GF=GH,∠AEH=∠BFE,证出四边形EFGH是菱形,再证出∠HEF=90°,即可得出结论;(2)直线EG经过正方形ABCD的中心, 连接BD交EG于点O,易证△EOB≌△GOD.可得BO=DO即点O为BD的中点.所以直线EG经过正方形ABCD的中心.
试题解析:
(![]() )∵四边形
)∵四边形![]() 是正方形.
是正方形.
∴![]() ,
, ![]() .
.
∵![]() .
.
∴![]() .
.
∴![]() ≌
≌![]() ≌
≌![]() ≌
≌![]() .
.
∴![]() ,
, ![]() .
.
∴四边形![]() 是菱形.
是菱形.
∵![]() ,
, ![]() .
.
∴![]() .
.
∴![]() .
.
∵四边形![]() 是菱形,
是菱形, ![]() .
.
∴四边形![]() 是正方形.
是正方形.
(![]() )直线
)直线![]() 经过正方形
经过正方形![]() 的中心,理由如下:
的中心,理由如下:
连接![]() 交
交![]() 于点
于点![]() .
.

∵四边形![]() 是正方形.
是正方形.
∴![]() .
.
∴![]() .
.
∵![]() ,
, ![]() ,
, ![]() .
.
∴![]() ≌
≌![]() .
.
∴![]() ,即点
,即点![]() 为
为![]() 的中点.
的中点.
∴直线![]() 经过正方形
经过正方形![]() 的中心.
的中心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】电线杆的支架做成三角形的,是利用三角形的_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在矩形ABCD中,AD=6㎝,AB=3㎝。在直角梯形中EFGH中 ,EH∥FG ,∠EFG=
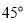 ,∠G=
,∠G=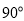 ,EH=6㎝,HG=3㎝。B、C、F、G同在一条直线上。当F、C两点重合时,矩形ABCD以1㎝/秒的速度沿直线按箭头所示的方向匀速平移,
,EH=6㎝,HG=3㎝。B、C、F、G同在一条直线上。当F、C两点重合时,矩形ABCD以1㎝/秒的速度沿直线按箭头所示的方向匀速平移, 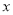 秒后,矩形ABCD与梯形EFGH重合部分的面积为
秒后,矩形ABCD与梯形EFGH重合部分的面积为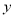 ㎝。按要求回答下列各题(不要求写出解题过程):
㎝。按要求回答下列各题(不要求写出解题过程):(1)当
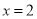 时,
时, 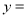 cm2(如图①);
cm2(如图①);当
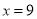 时,
时, 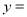 cm2(如图④);
cm2(如图④);(2)在下列各种情况下,分别用
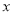 表示
表示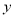 :
:如图①,当
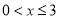 时,
时, 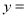 cm2;
cm2;如图②,当
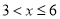 时,
时, 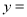 cm2;
cm2;如图③,当
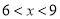 时,
时, 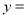 cm2;
cm2;如图⑤,当
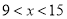 时,
时,  cm2.
cm2.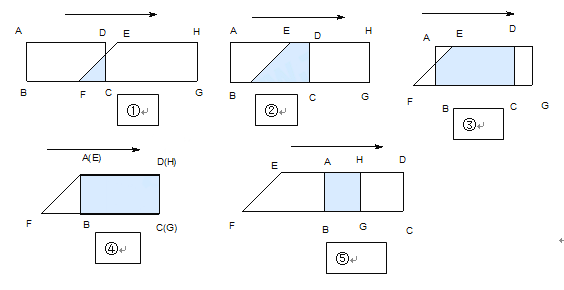
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各点中,在第四象限的点是( )
A.(-1,-4)B.(1,-4)C.(-1,0)D.(1,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系中的图像可能是 ( )
A.
 B.
B. 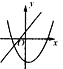 C.
C. 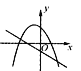 D.
D. 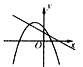
-
科目: 来源: 题型:
查看答案和解析>>【题目】某厂准备购买
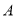 、
、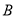 、
、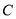 三种配件共
三种配件共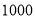 件,要求购买时
件,要求购买时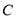 配件的件数是
配件的件数是 配件数的
配件数的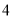 倍,
倍, 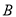 配件不超过
配件不超过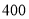 件,且每种配件都必须买,三种配件的价格如下:
件,且每种配件都必须买,三种配件的价格如下: 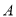 、
、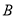 、
、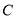 三种配件的单价分别为
三种配件的单价分别为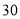 元、
元、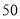 元、
元、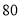 元.
元.(
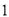 )求购买
)求购买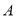 配件的件数范围.
配件的件数范围.(
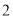 )三种配件应各买多少件,才能使买配件的总费用最少?总费用最少多少元?
)三种配件应各买多少件,才能使买配件的总费用最少?总费用最少多少元? -
科目: 来源: 题型:
查看答案和解析>>【题目】十边形的内角和是_____度.
相关试题

