搜索
【题目】如图，△ABC中，∠A=100°，BI、CI分别平分∠ABC，∠ACB，则∠BIC=________，若BM、CM分别平分∠ABC，∠ACB的外角平分线，则∠M=__________．
参考答案：
【答案】 140° 40°
【解析】∵∠A=100°，
∵∠ABC+∠ACB=180°100°=80°，
∵BI、CI分别平分∠ABC，∠ACB，
∴∠IBC=
∠ABC，∠ICB=
∠ACB，
∴∠IBC+∠ICB=
∠ABC+
∠ACB=
(∠ABC+∠ACB)= 
×80°=40°，
∴∠BIC=180°(∠IBC+∠ICB)=180°40°=140°，
∵∠ABC+∠ACB=80°，
∴∠DBC+∠ECB=180°∠ABC+180°∠ACB=360°(∠ABC+∠ACB)=360°80°=280°，
∵BM、CM分别平分∠ABC，∠ACB的外角平分线，
∴∠1=
∠DBC，∠2=
∠ECB，
∴∠1+∠2=
×280°=140°，
∴∠M=180°∠1∠2=40°.
故答案为：40°.
-
科目： 来源： 题型：
查看答案和解析>>【题目】甲、乙两同学进行数字猜谜游戏：甲说一个数a的相反数就是它本身，乙说一个数b的倒数也等于本身，请你猜一猜|a﹣b|=_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若(x-9)(2x-n)=2x2+mx-18，则m、n的值分别是( )
A. m=-16，n=-2B. m=16，n=-2C. m=-16，n=2D. m=16，n=2
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，点O为坐标原点，直线l与抛物线
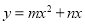相交于A（1，
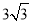），B（4，0）两点．（1）求出抛物线的解析式；
（2）在坐标轴上是否存在点D，使得△ABD是以线段AB为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；
（3）点P是线段AB上一动点，（点P不与点A、B重合），过点P作PM∥OA，交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN，求出
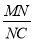的值，并求出此时点M的坐标．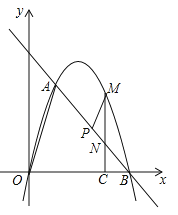
-
科目： 来源： 题型：
查看答案和解析>>【题目】某小组长统计组内6人一天在课堂上的发言次数分別为3，3，4，6，5，0．则这组数据的众数是( )
A. 3B. 3.5C. 4D. 5
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列结论正确的是（ ）
A.面积相等的两个三角形全等B.等边三角形都全等
C.底边和顶角对应相等的等腰三角形全等D.两个等腰直角三角形全等
-
科目： 来源： 题型：
查看答案和解析>>【题目】定义一种新运算：观察下列式子：1*3＝1×3﹣3＝0;3*（﹣1）＝3×3+1＝10;4*6＝4×3﹣6＝6;5*（﹣2）＝5×3+2＝17.（1）请你想一想：a*b＝______（2）（﹣7）*5＝______（3）若a*（﹣8）＝6*a请求出a的值
相关试题
