【题目】如图,矩形ABCD中,对角线AC,BD相交于O点,点P是线段AD上一动点(不与点D重合),PO的延长线交BC于Q点.
(1)求证:四边形PBQD为平行四边形.
(2)若AB=3cm,AD=4cm,P从点A出发.以1cm/s的速度向点D匀速运动.设点P的运动时间为ts,问:四边形PBQD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.

参考答案:
【答案】(1)证明见解析;(2)点P的运动时间为![]() s时,四边形PBQD能够成为菱形.
s时,四边形PBQD能够成为菱形.
【解析】试题分析:(1)证明△POD≌△QOB,得OP=OQ.,OD=OB,证明四边形PBQD是平行四边形.
(2)假设可以构成菱形,则PB=PD,在Rt△ABP中,AP2+AB2=PB2则可解得t=![]() .
.
试题解析:
(1)证明:∵四边形ABCD是矩形,∴AD∥BC,OD=OB.
∴∠PDO=∠QBO.
又∠POD=∠QOB,∴△POD≌△QOB.
∴OP=OQ.
∴四边形PBQD为平行四边形.
(2)解:能.点P从点A出发运动ts时,AP=tcm,PD=(4-t)cm.
当四边形PBQD是菱形时,PB=PD=(4-t)cm.
∵四边形ABCD是矩形,∴∠BAP=90°.
∴在Rt△ABP中,AP2+AB2=PB2,即t2+32=(4-t)2.解得t=![]() .
.
∴点P的运动时间为![]() s时,四边形PBQD能够成为菱形.
s时,四边形PBQD能够成为菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△ACD,连接AD,BC.若∠ACB=30°,AB=1,CC=x,则下列结论:①△AAD≌△CCB;②当x=1时,四边形ABCD是菱形;③当x=2时,△BDD为等边三角形.其中正确的是_______(填序号).

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,O是AC上一动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.若点O运动到AC的中点,则∠ACB=_____°时,四边形AECF是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.

(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
 为
为 上的一点,按下列要求进行作图.
上的一点,按下列要求进行作图.(1)作
 的平分线
的平分线 .
.(2)在
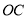 上取一点
上取一点 ,使得
,使得 .
.(3)爱动脑筋的小刚经过仔细观察后,进行如下操作:在边
 上取一点
上取一点 ,使得
,使得 ,这时他发现
,这时他发现 与
与 之间存在一定的数量关系,请写出
之间存在一定的数量关系,请写出 与
与 的数量关系,并说明理由.
的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】通过类比联想、引申拓展研究典型题目,可达到解一题知一类的目的.下面是一个案例.
原题:如图①,点
 分别在正方形
分别在正方形 的边
的边 上,
上,  ,连接
,连接 ,则
,则 ,试说明理由.
,试说明理由.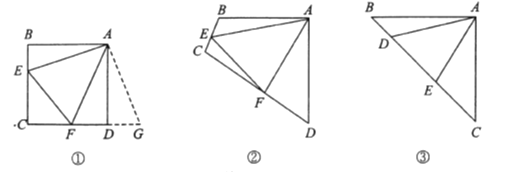
(1)思路梳理
因为
 ,所以把
,所以把 绕点
绕点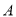 逆时针旋转90°至
逆时针旋转90°至 ,可使
,可使 与
与 重合.因为
重合.因为 ,所以
,所以 ,点
,点 共线.
共线.根据 ,易证
 ,得
,得 .请证明.
.请证明.(2)类比引申
如图②,四边形
 中,
中,  ,
,  ,点
,点 分别在边
分别在边 上,
上,  .若
.若 都不是直角,则当
都不是直角,则当 与
与 满足等量关系时,
满足等量关系时,  仍然成立,请证明.
仍然成立,请证明.(3)联想拓展
如图③,在
 中,
中,  ,点
,点 均在边
均在边 上,且
上,且 .猜想
.猜想 应满足的等量关系,并写出证明过程.
应满足的等量关系,并写出证明过程. -
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)x2-4x+2=0; (2)x2+3x+2=0;
(3)3x2-7x+4=0.
相关试题

