【题目】如图，抛物线经过A(－1,0)、B(3, 0)、C (0 ,3)三点。

（1）求抛物线的函数关系式；

（2）在抛物线上存在一点P，使△ABP的面积为8，请求出点P的坐标．

（3）在抛物线的对称轴上是否存在一点Q，使得QC+QA最短？若Q点存在，求出Q点的坐标；Q点不存在，请说明理由．

参考答案：

【答案】(1) ; (2) ; (3)存在，（3）Q（1，2）

【解析】试题分析:(1)因为抛物线经过与x轴的两个交点A(－1,0),

B(3,0),所以可设二次函数解析式为,将C (0 ,3)代入可求,所以二次函数解析式为.

(2)因为AB=4, △ABP的面积为8,根据三角形面积可求得高为4,则点P的纵坐标是4,-4,

令,可得: ,解得x的值,即点P的横坐标,

(3) 在抛物线的对称轴上找一点Q,使得QC+QA最短,根据二次函数图象的对称轴性可得:点A,B关于对称轴对称,连接BC,BC与对称轴的交点即为点Q,利用待定系数法求出直线BC的解析式,再求直线与对称轴的交点.

解：（1）∵二次函数y=ax+bx+c过点A(-1，0),B(3，0),C(0，3)

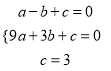，解得： ，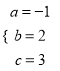

∴二次函数的解析式： .

（2）AB=4，

设△ABP的高为h，

∵△ABP的面积为8，

∴ AB·h=8,

解得：h=4，

当y=4时， ，

解得：x=1，

∴

当y=-4时， ，

∴

（3）Q（1，2）

关闭