Question

【题目】抛物线与直线相交于A、B 两点．

（1）求这条抛物线的解析式；

（2）若，求的最小值．

Answer 1

【答案】(1) y1=x2-2x-3；(2)-12.

【解析】试题分析：

(1) 利用点B的坐标可以求得直线解析式中m的值，从而确定直线的解析式. 利用直线的解析式可以求得点A的坐标. 将点A与点B的坐标代入抛物线解析式得到关于b和c的二元一次方程组，解这个方程组即可求得b和c的值，进而求得抛物线的解析式.

(2) 利用第(1)小题中求得的直线和抛物线的解析式，可以将y2-y1的值表示为x的二次函数. 通过对该二次函数增减性的分析可知，y2-y1只可能在当x=-4或x=1时取得最小值. 通过比较这两个条件下的函数值即可求得y2-y1的最小值.

试题解析：

(1) 由题意知，直线y2=-2x+m经过点B(2, -3)，将点B的坐标代入直线的解析式，得

，

∴m=1，

∴直线的解析式为y2=-2x+1.

由题意知，上述直线经过点A(-2, n)，将点A的坐标代入直线的解析式，得

，

∴n=5，

∴点A的坐标为(-2, 5).

由题意知，抛物线y1=x2+bx+c经过点A和点B，将点A与点B的坐标代入抛物线解析式，得

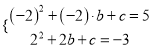,即，

解之，得

，

∴抛物线的解析式为y1=x2-2x-3.

(2) ∵抛物线y1=x2-2x-3，直线y2=-2x+1，

∴y2-y1=(-2x+1)-(x2-2x-3)=-x2+4.

由此可知，y2-y1的值是x的二次函数.

∵该二次函数图象的对称轴为y轴且抛物线开口向下，

∴当x<0时，y2-y1的值随x的增大而增大；当x>0时，y2-y1的值随x的增大而减小，

∵，

∴y2-y1只可能在当x=-4或x=1时取得最小值.

∵当x=-4时，y2-y1=-(-4)2+4=-12，

当x=1时，y2-y1=-12+4=3，

∴当x=-4时，y2-y1取最小值，最小值为-12.