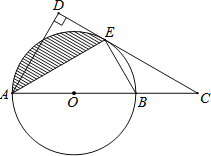
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°,求出图中阴影部分的面积.
参考答案:
【答案】(1)证明见解析;(2)![]()
【解析】试题分析:(1)连接OE,可证得OE∥AD,则∠DAE=∠AEO=∠EAO,可得结论;
(2)由条件求得∠AOE=120°,容易求得△AOE和扇形AOE的面积,利用面积差可求得阴影部分的面积.
试题解析:(1)证明:连接OE,如图,
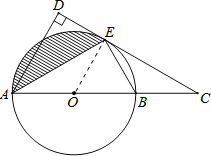
∵CD与⊙O相切于点E,
∴OE⊥CD,
∵AD⊥CD,
∴OE∥AD,
∴∠DAE=∠AEO,
∵AO=OE,
∴∠AEO=∠OAE,
∴∠OAE=∠DAE,
∴AE平分∠DAC;
(2)∵OA=OB,
∴∠AEO=∠OAE=30°,
∴∠AOE=120°,
∴阴影部分的面积=S扇形AOE﹣S△AOE
=S扇形AOE﹣![]() S△ABE
S△ABE
=![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知矩形的面积为1,设该矩形的长为x,周长为y,小彬借鉴以前研究函数的经验,对函数y随自变量x的变化进行了探究;以下是小彬的探究过程:
(1)结合问题情境分析: ①y与x的函数表达式为;②自变量x的取值范围是 .
(2)下表是y与x的几组对应值.x
…



1
2
3
4
…
y
…
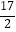
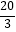
5
4
m
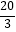
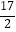
…
①写出m的值;
②画出函数图象;
③观察图象,写出该函数两条不同类型的性质. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是以BC为直径的半圆O的切线,D为半圆上一点,AD=AB,AD,BC的延长线相交于点E.
(1)求证:AD是半圆O的切线;
(2)连结CD,求证:∠A=2∠CDE;
(3)若∠CDE=30°,OB=2,求
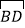 的长.
的长.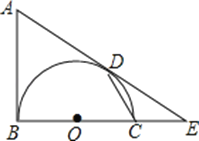
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明在计算一个多项式加上5ab+4bc﹣3ac,不小心看成减去5ab+4bc﹣3ac,计算出结果为3ab﹣4bc+5ac,试求出原题目的正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2017年的“双11”网上促销活动中,淘宝网的交易额突破了3200000000元,将数字3200000000用科学记数法表示 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若M=(a+3)(a-4),N=(a+2)(2a-5),其中a为有理数,则M、N的大小关系是( )
A. M>N B. M<N C. M=N D. 无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知M(2)=(-2)×(-2),
M(3)=(-2)×(-2)×(-2),
…,
M(n)=
 .
.(1)计算:M(5)+M(6);
(2)求2M(2 016)+M(2 017)的值;
(3)说明2M(n)与M(n+1)互为相反数.
相关试题

