【题目】已知二次函数y=x2﹣2x+c(c<0)的图象与x轴交于A,B两点(A点在B点的左侧),与y轴交于点C,且OB=OC.
(Ⅰ)求该抛物线的解析式和顶点坐标;
(Ⅱ)直线l是抛物线的对称轴,E是抛物线的顶点,连接BE,线段OC上的点F关于直线l的对称点F′恰好在线段BE上,求点F的坐标;
(Ⅲ)若有动点P在线段OB上,过点P作x轴的垂线分别与BC交于点M,与抛物线交于点N,试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段NQ的长度最小?如果存在,求出点Q的坐标;如果不存在,说明理由.
参考答案:
【答案】(Ⅰ)y=x2﹣2x﹣3;(1,﹣4);(Ⅱ)点F的坐标为(0,﹣2);(Ⅲ)存在,满足题意的点Q的坐标为![]() 和
和![]() .
.
【解析】分析:
(1)由已知条件易得点C的坐标为(0,c),结合OB=OC,点A在点B的左侧可得点B的坐标为(-c,0),把点B的坐标(-c,0)代入y=x2﹣2x+c中结合c<0即可求得c的值,从而得到抛物线的解析式,将所得解析式化为顶点式即可得到抛物线的顶点坐标;
(2)由(1)可知抛物线的对称轴为直线x=1,设点F的坐标为(0,m),则点F′的坐标为(2,m),由(1)可得点B、E的坐标,则由此可求得直线BE的解析式,把F′的坐标代入所得BE的解析式即可求得m的值,从而可得此时点F的坐标;
(3)如下图,设点P的坐标为(n,0),则PA=n+1,PB=PM=3﹣n,PN=﹣n2+2n-3,
作QR⊥PN,垂足为R,由S△PQN=S△APM,可得![]() (n+1)(3﹣n)=
(n+1)(3﹣n)=![]() (﹣n2+2n+3)QR化简整理可得:QR=1,然后分点Q在PN的右侧和左侧两种情况分别用含n的式子表达出点R和N的坐标,然后在Rt△QRN中由勾股定理用含n的式子表达出NQ2,即可求得NQ最小时n的值,由此即可求出对应的点Q的坐标了.
(﹣n2+2n+3)QR化简整理可得:QR=1,然后分点Q在PN的右侧和左侧两种情况分别用含n的式子表达出点R和N的坐标,然后在Rt△QRN中由勾股定理用含n的式子表达出NQ2,即可求得NQ最小时n的值,由此即可求出对应的点Q的坐标了.
详解:
(Ⅰ)∵y=x2﹣2x+c(c<0),
∴点C的坐标为(0,c),
∵OB=OC,点A在点B的左侧,
∴点B的坐标为(﹣c,0),
将(﹣c,0)代入y=x2﹣2x+c,
解得c=﹣3或c=0(舍去)
∴c=﹣3,
∴抛物线的解析式为y=x2﹣2x﹣3,配方得y=(x﹣1)2﹣4,
∴顶点坐标为(1,﹣4);
(Ⅱ)设点F的坐标为(0,m),
∵对称轴为直线l:x=1,
∴点F关于直线的对称点F′的坐标为(2,m),
设直线BE的解析式为y=kx+b,
由(1)可知点B、E的坐标分别为(3,0),(1,﹣4),将两个坐标代入y=kx+b得:
![]() ,解得
,解得![]() ,
,
∴直线BE的解析式为y=2x﹣6,
∵点F′在直线BE上,
∴m=2×2﹣6=﹣2,
∴点F的坐标为(0,﹣2);
(Ⅲ)存在,
如下图所示,设点P的坐标为(n,0),
则PA=n+1,PB=PM=3﹣n,PN=﹣n2+2n-3,
作QR⊥PN,垂足为R,
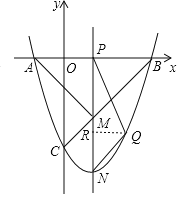
∵S△PQN=S△APM,
∴![]() (n+1)(3﹣n)=
(n+1)(3﹣n)=![]() (﹣n2+2n+3)QR,
(﹣n2+2n+3)QR,
∴QR=1,
①点Q在直线PN的右侧时,Q点坐标为(n+1,n2﹣4),R点的坐标为(n,n2﹣4),N点的坐标为(n,n2﹣2n﹣3),
∴QR=1,RN=2n-1,
∴在Rt△QNR中,NQ2=1+(2n﹣1)2,
∴当n=![]() 时,NQ取最小值,此时Q点的坐标为
时,NQ取最小值,此时Q点的坐标为![]() ,
,
②点Q在直线PN的左侧时,Q点的坐标为(n﹣1,n2﹣4n)
同①可得:NQ2=1+(-2n+3)2,
∴当n=![]() 时,NQ取最小值,此时Q点的坐标为
时,NQ取最小值,此时Q点的坐标为![]() ,
,
综上所述,满足题意点Q坐标为![]() 和
和![]() .
.
-
科目: 来源: 题型:
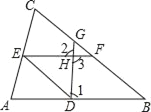
查看答案和解析>>【题目】完成下面的证明过程
如图,已知∠1+∠2=180°,∠B=∠DEF,求证:DE∥BC.
证明:∵∠1+∠2=180°(已知),
而∠2=∠3(________),
∴∠1+∠3=180°
∴______∥______(________)
∴∠B=______(________)
∵∠B=∠DEF(已知)
∴∠DEF=______(等量代换)
∴DE∥BC(________)
-
科目: 来源: 题型:
查看答案和解析>>【题目】为创建足球特色学校,营造足球文化氛围,某学校随机抽取部分八年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分—10分,B级:7分—7.9分,C级:6分—6.9分,D级:1分—5.9分)根据所给信息,解答以下问题:
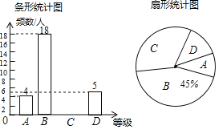
(1)样本容量为 ,C对应的扇形的圆心角是____度,补全条形统计图;
(2)所抽取学生的足球运球测试成绩的中位数会落在____等级;
(3)该校八年级有300名学生,请估计足球运球测试成绩达到
 级的学生有多少人?
级的学生有多少人? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平行四边形ABCD中,DB=DA,∠ADB的平分线交AB于点F,交CB的延长线于点E,连接AE.
(1)求证:四边形AEBD是菱形;
(2)若DC=
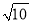 ,EF:BF=3,求菱形AEBD的面积.
,EF:BF=3,求菱形AEBD的面积.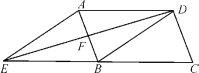
-
科目: 来源: 题型:
查看答案和解析>>【题目】为方便市民出行,减轻城市中心交通压力,贵阳市地铁1号线于2018年12月1号正式全线开通.地铁开通后,李明爸爸妈妈的出行方式将由乘公交车改为乘坐地铁,爸爸从国际生态会议中心站出发至喷水池站,每天所需的时间将比以往节省70%;妈妈从国际生态会议中心站出发至珠江路站,每天所需的时间将比以往节省55%,这样两人所需的时间共节省60%,现在两人乘地铁所需的时间之和为1.2小时.请问李明爸爸妈妈原来乘公交车上班时每天所需时间各为多少小时?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一个坡角为40°的斜坡上有一棵树BC,树高4米.当太阳光AC与水平线成70°角时,该树在斜坡上的树影恰好为线段AB,求树影AB的长.(结果保留一位小数)
(参考数据:sin20°=0.34,tan20°=0.36,sin30°=0.50,tan30°=0.58,sin40°=0.64,tan40°=0.84,sin70°=0.94,tan70°=2.75)
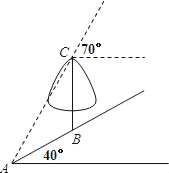
-
科目: 来源: 题型:
查看答案和解析>>【题目】某天上午,一出租车司机始终在一条南北走向的笔直马路上营运,(出发点记作为点O,约定向南为正,向北为负),期间一共运载6名乘客,行车里程(单位:千米)依先后次序记录如下:﹢7,﹣3,﹢6,﹣1,﹢2,﹣4.
(1)出租车在行驶过程中,离出发点O最远的距离是______千米;
(2)将最后一名乘客送到目的地,出租车离出发点O多远?在O点的什么方向?
(3)出租车收费标准为:起步价(不超过3千米)为8元,超过3千米的部分每千米的价格为1.5元,求司机这天上午的营业额.
相关试题

