【题目】已知二次函数y=ax2+bx+c的图象对称轴为x=![]() ,图象交x轴于A,B,交y轴于C(0,-3),且AB=5,直线y=kx+b(k>0)与二次函数图象交于M,N(M在N的右边),交y轴于P.
,图象交x轴于A,B,交y轴于C(0,-3),且AB=5,直线y=kx+b(k>0)与二次函数图象交于M,N(M在N的右边),交y轴于P.
(1)求二次函数图象的解析式;
(2)若b=-5,且△CMN的面积为3,求k的值;
(3)若b=-3k,直线AN交y轴于Q,求![]() 的值或取值范围.
的值或取值范围.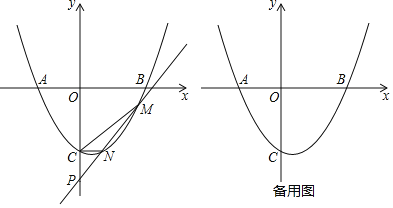
参考答案:
【答案】(1)![]() ;(2)k=2;(3)
;(2)k=2;(3)![]() ≥
≥![]() .
.
【解析】
(1)由图象对称轴为x=![]() ,AB=5,知:A(-2,0)、B(0,-3),把A、B、C点坐标代入二次函数即可求解;
,AB=5,知:A(-2,0)、B(0,-3),把A、B、C点坐标代入二次函数即可求解;
(2)S△CMN=![]() HNxM=6,用根与系数的关系求解即可;
HNxM=6,用根与系数的关系求解即可;
(3)求出xN=![]() ,分2k-5>0时和2k-5<0两种情况,求出点Q坐标即可求解.
,分2k-5>0时和2k-5<0两种情况,求出点Q坐标即可求解.
(1)由图象对称轴为x=![]() ,AB=5,知:A(-2,0)、B(0,-3),
,AB=5,知:A(-2,0)、B(0,-3),
把A、B、C点坐标代入二次函数表达式得:a=![]() ,b=-
,b=-![]() ,c=-3;
,c=-3;
故函数表达式为:y=![]() x2-
x2-![]() x-3…①;
x-3…①;
(2)b=-5,直线MN表达式为:y=kx-5…②,
设:M(x1,y1),N(x2,y2),
将①、②联立并整理得:x2-(2k+1)x+4=0,
则:x1+x2=2k+1,x1x2=4,
直线C(0,-3)、M(x1,y1)所在的直线方程为:
y=![]() ,
,
过N点做直线HM∥y轴,交MC于H,则H(x1,![]() x13),
x13),
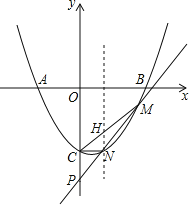
S△CMN=![]() HNxM=6,
HNxM=6,
整理得:x1y2-x2y1+3x1-3x2=6,
把y1=3x1-5,y2=3x2-5,代入上式整理得:
x2-x1=3,
即:(x1+x2)2-4x1x2=9,
k=2;
(3)b=-3k,直线y=kx+b=kx-3k…③,
将①、③方程联立并整理得:
x2-(2k+1)x+(6k-6)=0,
△=4k2-20k+25=(2k-5)2>0,
xN=![]() ,
,
当2k-5>0时,
xN=3,则N(3,0),
而Q(0,0),P(0,-3k),C(0,-3)
则:CP=3k-3,CQ=3,
∴![]() =k-1,即:
=k-1,即:![]() >
>![]() ;
;
当2k-5<0时,
xN=2k-2,则N(2k-2,2k2-5k),
则AN所在的直线方程为:y=![]() x+(2k5),
x+(2k5),
则:Q(0,2k-5),
而C(0,-3)P(0,-3k),
则:CP=3k-3,CQ=2k-2,
∴![]() =
=![]() ,
,
故:![]() ≥
≥![]() .
.
-
科目: 来源: 题型:
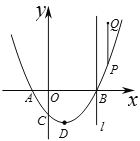
查看答案和解析>>【题目】如图,已知抛物线L1:y=
 x2-x-
x2-x- ,L1交x轴于A,B(点A在点B左边),交y轴于C,其顶点为D,P是L1上一个动点,过P沿y轴正方向作线段PQ∥y轴,使PQ=t,当P点在L1上运动时,Q随之运动形成的图形记为L2.
,L1交x轴于A,B(点A在点B左边),交y轴于C,其顶点为D,P是L1上一个动点,过P沿y轴正方向作线段PQ∥y轴,使PQ=t,当P点在L1上运动时,Q随之运动形成的图形记为L2.(1)若t=3,求图形L2的函数解析式;
(2)过B作直线l∥y轴,若直线l和y轴及L1,L2所围成的图形面积为12,求t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】上周六上午
 点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离
点,小颖同爸爸妈妈一起从西安出发回安康看望姥姥,途中他们在一个服务区休息了半小时,然后直达姥姥家,如图,是小颖一家这次行程中距姥姥家的距离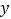 (千米)与他们路途所用的时间
(千米)与他们路途所用的时间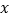 (时)之间的函数图象,请根据以上信息,解答下列问题:
(时)之间的函数图象,请根据以上信息,解答下列问题:(1)求直线
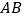 所对应的函数关系式;
所对应的函数关系式;(2)已知小颖一家出服务区后,行驶
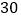 分钟时,距姥姥家还有
分钟时,距姥姥家还有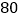 千米,问小颖一家当天几点到达姥姥家?
千米,问小颖一家当天几点到达姥姥家?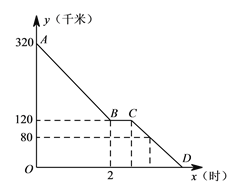
-
科目: 来源: 题型:
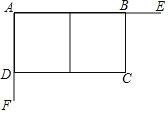
查看答案和解析>>【题目】如图,某工程队在工地互相垂直的两面墙AE、AF处,用180米长的铁栅栏围成一个长方形场地ABCD,中间用同样材料分割成两个长方形.已知墙AE长120米,墙AF长40米,要使长方形ABCD的面积为4000平方米,问BC和CD各取多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,⊙O过正方形ABCD的顶点A、D且与边BC相切于点E,分别交AB、DC于点M、N.动点P在⊙O或正方形ABCD的边上以每秒一个单位的速度做连续匀速运动.设运动的时间为x,圆心O与P点的距离为y,图2记录了一段时间里y与x的函数关系,在这段时间里P点的运动路径为( )

A. 从D点出发,沿弧DA→弧AM→线段BM→线段BC
B. 从B点出发,沿线段BC→线段CN→弧ND→弧DA
C. 从A点出发,沿弧AM→线段BM→线段BC→线段CN
D. 从C点出发,沿线段CN→弧ND→弧DA→线段AB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC绕点C顺时针旋转90°得到△EDC.若点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是

A. 55° B. 60° C. 65° D. 70°
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知等腰三角形ABC的底角为30°,以BC为直径的⊙O与底边AB交于点D,过D作DE⊥AC,垂足为E.
(1)证明:DE为⊙O的切线;
(2)连接OE,若BC=4,求△OEC的面积.

相关试题

