【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=![]() ;
;
(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
【答案】(1)原式= 2a2+b2=2+2=4;(2)原式=4.
【解析】试题分析:(1)利用完全平方公式展开,化简,代入求值. (2) 利用完全平方公式展开,化简,整体代入求值.
解:(1)原式=a2-2ab+a2+2ab+b2=2a2+b2.
当a=-1,b=![]() 时,原式=2+2=4.
时,原式=2+2=4.
(2)原式=2x2-3x+1-(x2+2x+1)+1=x2-5x+1=3+1=4.
【题型】解答题
【结束】
22
【题目】已知化简(x2+px+8)(x2-3x+q)的结果中不含x2项和x3项.
(1)求p,q的值.
(2)x2-2px+3q是否是完全平方式?如果是,请将其分解因式;如果不是,请说明理由.
参考答案:
【答案】(1)![]() ;(2)x2-2px+3q不是完全平方式.理由见解析.
;(2)x2-2px+3q不是完全平方式.理由见解析.
【解析】试题分析:(1)展开,化简,让x2项和x3项系数为0.
(2)把(1)中结论代入,不满足完全平方公式.
试题解析:
解:(1)原式=x4+(-3+p)x3+(q-3p+8)x2+(pq-24)x+8q.
∵结果中不含x2项和x3项,∴ ![]()
解得![]()
(2)x2-2px+3q不是完全平方式.理由如下:
把![]() 代入x2-2px+3q,得x2-2px+3q=x2-6x+3.
代入x2-2px+3q,得x2-2px+3q=x2-6x+3.
∵x2-6x+9是完全平方式,∴x2-6x+3不是完全平方式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c的图象如图所示,下列结论:①b<2a;②a+2c﹣b>0;③b>a>c;④b2+2ac<3ab.其中正确结论的个数是( )
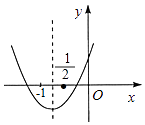
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)992-102×98;
(2)[x(x2y2-xy)-y(x2-x3y)]÷x2y.
【答案】(1)-195(2)2xy-2
【解析】试题分析:(1)利用平方差公式,完全平方公式简便计算.
(2)提取公因式,化简.
试题解析:
(1)原式=(100-1)2-(100+2)×(100-2)
=(1002-200+1)-(1002-4)=-200+5=-195.
(2)原式=[x2y(xy-1)-x2y(1-xy)]÷x2y
=2x2y(xy-1)÷x2y=2(xy-1)=2xy-2.
【题型】解答题
【结束】
21【题目】(1)先化简,再求值:a(a-2b)+(a+b)2,其中a=-1,b=
 ;
;(2)若x2-5x=3,求(x-1)(2x-1)-(x+1)2+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一条直线上任取一点A,截取AB=20 cm,再截取AC=18 cm,M,N分别是AB,AC的中点,求M,N两点之间的距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
=y2+8y+16 (第二步)
=(y+4)2(第三步)
=(x2-4x+4)2(第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式
B.平方差公式
C.两数和的完全平方公式
D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)若不彻底,请直接写出因式分解的最后结果_________ .
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①是棱长为a的小正方体,如图②、如图③是由若干这样相同的小正方体摆放而成,按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n层,第n层中小正方体的个数为s(提示:第一层中,s=1;第二层中,s=3),则第n层中,s=________.(用含n的式子表示)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C是线段AB上一点,M是线段AC的中点,N是线段BC的中点.
(1)如果AB=20 cm,AM=6 cm,求NC的长;
(2)如果MN=6 cm,求AB的长.

相关试题

