【题目】在平面直角坐标系中,已知点A、B的坐标分别为A(6,0)、B(0,2),以AB为斜边在右上方作Rt△ABC.设点C坐标为(x,y),则(x+y)的最大值= . 
参考答案:
【答案】4+2 ![]()
【解析】解:由题可得,点C在以AB为直径的⊙D上运动, 点C坐标为(x,y),可构造新的函数x+y=m,则函数与y轴交点最高处即为x+y的最大值,
此时,直线y=﹣x+m与⊙D相切,交x轴与E,如图所示,
连接OD,CD,
∵A(6,0)、B(0,2),
∴D(3,1),
∴OD= ![]() =
= ![]() ,
,
∴CD= ![]() ,
,
根据两点间的距离可得,C(3+ ![]() ,1+
,1+ ![]() ),
),
代入直线y=﹣x+m,可得
1+ ![]() =﹣(3+
=﹣(3+ ![]() )+m,
)+m,
解得m=4+2 ![]() ,
,
∴x+y的最大值为4+2 ![]() ,
,
故答案为:4+2 ![]() .
.
根据以AB为斜边在右上方作Rt△ABC,可知点C在以AB为直径的⊙D上运动,根据点C坐标为(x,y),可构造新的函数x+y=m,则函数与y轴交点最高处即为x+y的最大值,此时,直线y=﹣x+m与⊙D相切,再根据圆心点D的坐标,可得C的坐标为(3+ ![]() ,1+
,1+ ![]() ),代入直线y=﹣x+m,可得m=4+2
),代入直线y=﹣x+m,可得m=4+2 ![]() ,即可得出x+y的最大值为4+2
,即可得出x+y的最大值为4+2 ![]() .
.
-
科目: 来源: 题型:
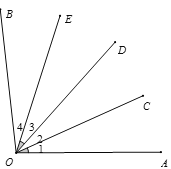
查看答案和解析>>【题目】如图所示,∠1=∠2=∠3=∠4=24°,根据图形填空:
(1)是∠2的3倍的角是_________________(用字母表示)
(2)是∠AOD的
 的角有_________个;
的角有_________个;(3)射线OC是哪个角的3等分线?又是哪个角的4等分线?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是一个圆,一只电子跳蚤在标有数字的五个点上跳跃.若它停在奇数点上时,则一次沿顺时针方向跳两个点;若停在偶数点上时,则下一次沿逆时针方向跳一个点.若这只跳蚤从1这点开始跳,则经过2019次跳后它所停在的点对应的数为( )
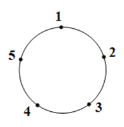
A. 1 B. 2 C. 4 D. 5
-
科目: 来源: 题型:
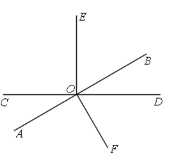
查看答案和解析>>【题目】已知如图,直线AB、CD相交于点O,∠COE=90°,若∠BOD:∠BOC=1:5.
(1)求∠AOC的度数;
(2)如图,过点O作OF⊥AB,求∠DOF与∠EOF的度数.
-
科目: 来源: 题型:
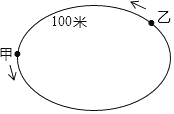
查看答案和解析>>【题目】已知甲沿周长为300米的环形跑道按逆时针方向跑步,速度为a米/秒,与此同时在甲后面100米的乙也沿该环形跑道按逆时针方向跑步,速度为3米/秒.
(1)若a=1,求甲、乙两人第一次相遇所用的时间;
(2)若a>3,甲、乙两人第一次相遇所用的时间为80秒,试求a的值.
-
科目: 来源: 题型:
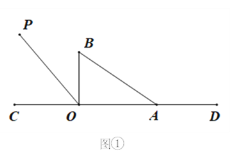
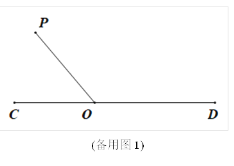
查看答案和解析>>【题目】如图①,直线CD上有一点O,过点O在直线CD上方作射线OP.将一直角三角尺AOB(∠AOB=90°)的直角顶点放在点O处,一条直角边OA在射线OD上,另一边OB在直线CD上方.将直角三角板绕着点O逆时针旋转.
(1)当直角三角板旋转到如图②的位置,OB恰好平分∠COP时,试证明:OA边恰好平分∠POD.
(2)若射线OP的位置保持不变,且∠COP=50°.当直角三角尺旋转到边AB与射线OC相交时则∠BOC与∠AOP有怎样的数量关系?试画出图形,写出数量关系,并写出说理过程.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:分式和分数有着很多的相似点.如类比分数的基本性质,我们得到了分式的基本性质;类比分数的运算法则,我们得到了分式的运算法则;等等.小学里,把分子比分母小的分数叫做真分数.类似地,我们把分子整式的次数小于分母整式的次数的分式称为真分式;反之,称为假分式.任何一个假分式都可以化成整式与真分式的和的形式,如:
 ;
; 
(1)下列分式中,属于真分式的是:________(填序号);
①
 ②
② ③
③ ④
④
(2)将假分式
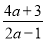 化成整式与真分式的和的形式:
化成整式与真分式的和的形式:  =________+________;
=________+________;(3)将假分式
 化成整式与真分式的和的形式:
化成整式与真分式的和的形式:  =__________________.
=__________________.
相关试题

