【题目】如图,已知∠1=∠2,∠3=∠4,∠E=90°,试问:AB∥CD吗?为什么?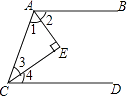
解:∵∠1+∠3+∠E=180°∠E=90°
∴∠1+∠3=
∵∠1=∠2,∠3=∠4
∴∠1+∠2+∠3+∠4=
∴AB∥CD .
参考答案:
【答案】180°;已知;90°;已知;180°;同旁内角互补两直线平行
【解析】∵∠1+∠3+∠E=180°∠E=90° (已知),
∴∠1+∠3=90°,
∵∠1=∠2,∠3=∠4 (已知),
∴∠1+∠2+∠3+∠4=180°,
∴AB∥CD (同旁内角互补两直线平行).
所以答案是:180°、90°已知、已知、180°、同旁内角互补两直线平行.
【考点精析】掌握平行线的判定和三角形的内角和外角是解答本题的根本,需要知道同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是BC的中点,AB⊥BC,DC⊥BC,AE平分∠BAD,下列结论:
①∠AED=90° ②∠ADE=∠CDE ③DE=BE ④AD=AB+CD,
四个结论中成立的是( )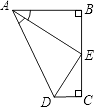
A.①②④
B.①②③
C.②③④
D.①③ -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件中:
①∠B+∠BCD=180°;
②∠1=∠2;
③∠3=∠4;
④∠B=∠5.
能判定AB∥CD的条件个数有( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的箱子里装有红色、蓝色、黄色的球共20个,除颜色外,形状、大小、质地等完全相同,小明通过多次摸球实验后发现摸到红色、黄色球的频率分别稳定在20%和35%,则箱子里蓝色球的个数很可能是______个.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某车队要把4000吨货物运到雅安地震灾区(方案定后,每天的运量不变)。
(1)从运输开始,每天运输的货物吨数n(单位:吨)与运输时间t(单位:天)之间有怎样的函数关系式?
(2)因地震,到灾区的道路受阻,实际每天比原计划少运20%,则推迟1天完成任务,求原计划完成任务的天数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知点A是双曲线
 在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线
在第三象限分支上的一个动点,连结AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,且随着点A的运动,点C的位置也在不断变化,但点C始终在双曲线 上运动,则k的值是 .
上运动,则k的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
①∠ACD=30°;②SABCD=ACBC;③OE:AC=
 :6;④S△OCF=2S△OEF
:6;④S△OCF=2S△OEF成立的个数有( )

A.1个 B.2个 C.3个 D.4个
相关试题

