【题目】如图,已知二次函数y=x2+mx+n的图象经过A(0,3),且对称轴是直线x=2.
(1)求该函数的解析式;
(2)在抛物线上找一点P,使△PBC的面积是△ABC的面积的![]() ,求出点P的坐标.
,求出点P的坐标.

参考答案:
【答案】(1)y=x2-4x+3;(2)点P的坐标是(2+![]() ,2)或(2-
,2)或(2-![]() ,2)
,2)
【解析】
试题(1)由A点坐标可知![]() ,由对称轴可知
,由对称轴可知![]() ,得到
,得到![]() ,从而得到函数的解析式为
,从而得到函数的解析式为![]() .
.
(2)根据坐标先求出△ABC的面积,进而求出△PBC的面积,根据三角形面积计算公式逆推出P点的纵坐标![]() ,再令
,再令![]() ,解一元二次方程即可求得P点的横坐标,从而得到P点坐标.
,解一元二次方程即可求得P点的横坐标,从而得到P点坐标.
试题解析:(1)由题意得n=3,![]() ,∴m=-4,∴该函数的解析式为y=x2-4x+3.
,∴m=-4,∴该函数的解析式为y=x2-4x+3.
(2)∵A(0,3),∴OA=3.∵S△PBC=![]() S△ABC,∴|yP|=
S△ABC,∴|yP|=![]() ×3=2.
×3=2.
∵函数的最小值为-1,∴yP=2.代入函数解析式中得x2-4x+3=2,解得x=2±![]() ,
,
∴点P的坐标是(2+![]() ,2)或(2-
,2)或(2-![]() ,2).
,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国从2008年6月起执行“限塑令”,“限塑令”执行前,某校为了了解本校学生所在家庭使用塑料袋的情况,随机调查了10名学生所在家庭月使用塑料袋的数量,结果如下(单位:只):
65,70,85,75,85,79,74,91,81,95
(1)计算这10名学生所在家庭平均月使用塑料袋多少只?
(2)“限塑令”执行后,家庭平均月使用塑料袋数量预计减少
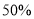 ,根据上面的计算后,你估计该校2000名学生所在的家庭平均月使用塑料袋一共可减少多少只?
,根据上面的计算后,你估计该校2000名学生所在的家庭平均月使用塑料袋一共可减少多少只? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点P为定角∠AOB的平分线上的一个定点,且∠MPN与∠AOB互补,若∠MPN在绕点P旋转的过程中,其两边分别与OA、OB相交于M、N两点,则以下结论:(1)PM=PN恒成立;(2)OM+ON的值不变;(3)四边形PMON的面积不变;(4)MN的长不变,其中正确的个数为( )

A. 4B. 3C. 2D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出A′、B′、C′的坐标,并在图中画出平移后图形;
(3)求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
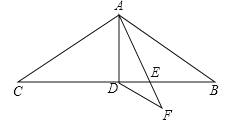
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果抛物线y=ax2+bx+c过定点M(1,0),则称此抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的解析式.小敏写出了一个正确的答案:y=2x2+3x-5.请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c,求该抛物线的顶点最低时的解析式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:△ADE为等边三角形.
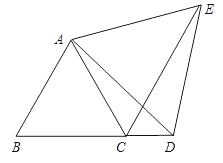
相关试题

