【题目】如果抛物线y=ax2+bx+c过定点M(1,0),则称此抛物线为定点抛物线.
(1)张老师在投影屏幕上出示了一个题目:请你写出一条定点抛物线的解析式.小敏写出了一个正确的答案:y=2x2+3x-5.请你写出一个不同于小敏的答案;
(2)张老师又在投影屏幕上出示了一个思考题:已知定点抛物线y=-x2+2bx+c,求该抛物线的顶点最低时的解析式.
参考答案:
【答案】(1)y=x2+3x-4(答案不唯一);(2)y=-x2+2x-1
【解析】
试题⑴将M点代入解析式可得![]() ,则只要系数满足
,则只要系数满足![]() 的解析式均可.
的解析式均可.
⑵由解析式是定点抛物线可知![]() ,解得
,解得![]() ,而抛物线顶点纵坐标为
,而抛物线顶点纵坐标为![]() ,将上式代入得
,将上式代入得![]() ,那么由抛物线顶点最低,可得
,那么由抛物线顶点最低,可得![]() ,解得
,解得![]() ,从而
,从而![]() ,解析式为
,解析式为![]() .
.
试题解析:(1) y=x2+3x-4(答案不唯一).
(2)∵y=-x2+2bx+c是定点抛物线,∴-1+2b+c=0,∴c=1-2b.∴该抛物线的顶点的纵坐标为![]() =
=![]() =c+b2=1-2b+b2=(b-1)2.当抛物线y=-x2+2bx+c的顶点最低时,即(b-1)2的值最小,最小值是0,这时b=1,c=1-2b=-1,∴抛物线的顶点最低时的解析式是y=-x2+2x-1.
=c+b2=1-2b+b2=(b-1)2.当抛物线y=-x2+2bx+c的顶点最低时,即(b-1)2的值最小,最小值是0,这时b=1,c=1-2b=-1,∴抛物线的顶点最低时的解析式是y=-x2+2x-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC在直角坐标系中,

(1)请写出△ABC各顶点的坐标;
(2)若把△ABC向上平移2个单位,再向左平移1个单位得到△A′B′C′,写出A′、B′、C′的坐标,并在图中画出平移后图形;
(3)求出△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知二次函数y=x2+mx+n的图象经过A(0,3),且对称轴是直线x=2.
(1)求该函数的解析式;
(2)在抛物线上找一点P,使△PBC的面积是△ABC的面积的
 ,求出点P的坐标.
,求出点P的坐标.
-
科目: 来源: 题型:
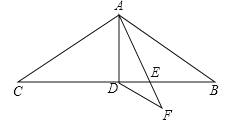
查看答案和解析>>【题目】如图在△ABC中,AB=AC=9,∠BAC=120°,AD是△ABC的中线,AE是∠BAD的角平分线,DF∥AB交AE的延长线于点F,求DF的长.
-
科目: 来源: 题型:
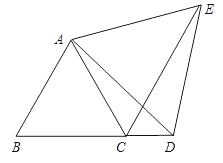
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,D为BC延长线上的一点,CE平分∠ACD,CE=BD,求证:△ADE为等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AC、BD是菱形ABCD的对角线,那么下列结论一定正确的是( )

A. △ABD与△ABC的周长相等
B. △ABD与△ABC的面积相等
C. 菱形的周长等于两条对角线之和的两倍
D. 菱形的面积等于两条对角线之积的两倍
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD中,F是BC上任意一点,连接AF交对角线BD于点E,连接EC.

(1)求证:AE=EC;
(2)当∠ABC=60°,∠CEF=60°时,点F在线段BC上的什么位置?说明理由.
相关试题

