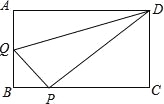
【题目】(2016宁夏第26题)在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
参考答案:
【答案】(1)、S=![]() (x﹣2)2+4;x=2,最小值为4;(2)、存在,理由见解析.
(x﹣2)2+4;x=2,最小值为4;(2)、存在,理由见解析.
【解析】
试题分析:(1)、可用x表示出AQ、BQ、BP、CP,从而可表示出S△ADQ、S△BPQ、S△PCD的面积,则可表示出S,再利用二次函数的增减性可求得是否有最大值,并能求得其最小值;(2)、用x表示出BQ、BP、PC,当QP⊥DP时,可证明△BPQ∽△CDP,利用相似三角形的性质可得到关于x的方程,可求得x的值.
试题解析:(1)、∵四边形ABCD为矩形, ∴BC=AD=4,CD=AB=3, 当运动x秒时,则AQ=x,BP=x,
∴BQ=AB﹣AQ=3﹣x,CP=BC﹣BP=4﹣x,
∴S△ADQ=![]() ADAQ=
ADAQ=![]() ×4x=2x,S△BPQ=
×4x=2x,S△BPQ=![]() BQBP=
BQBP=![]() (3﹣x)x=
(3﹣x)x=![]() x﹣
x﹣![]() x2,S△PCD=
x2,S△PCD=![]() PCCD=
PCCD=![]() (4﹣x)3=6﹣
(4﹣x)3=6﹣![]() x,
x,
又S矩形ABCD=ABBC=3×4=12,
∴S=S矩形ABCD﹣S△ADQ﹣S△BPQ﹣S△PCD=12﹣2x﹣(![]() x﹣
x﹣![]() x2)﹣(6﹣
x2)﹣(6﹣![]() x)=
x)=![]() x2﹣2x+6=
x2﹣2x+6=![]() (x﹣2)2+4,
(x﹣2)2+4,
即S=![]() (x﹣2)2+4, ∴S为开口向上的二次函数,且对称轴为x=2,
(x﹣2)2+4, ∴S为开口向上的二次函数,且对称轴为x=2,
∴当0<x<2时,S随x的增大而减小,当2<x≤3时,S随x的增大而增大,
又当x=0时,S=5,当S=3时,S=![]() ,但x的范围内取不到x=0,
,但x的范围内取不到x=0,
∴S不存在最大值,当x=2时,S有最小值,最小值为4;
(2)、存在,理由如下:
由(1)可知BQ=3﹣x,BP=x,CP=4﹣x, 当QP⊥DP时,则∠BPQ+∠DPC=∠DPC+∠PDC,
∴∠BPQ=∠PDC,且∠B=∠C, ∴△BPQ∽△PCD,
∴![]() =,即
=,即![]() =
=![]() ,解得x=
,解得x=![]() (舍去)或x=
(舍去)或x=![]() ,
,
∴当x=![]() 时QP⊥DP.
时QP⊥DP.
-
科目: 来源: 题型:
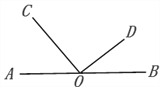
查看答案和解析>>【题目】如图,O是直线AB上的一点,OC⊥OD,垂足为O.
(1)若∠BOD=32°,求∠AOC的度数;
(2)若∠AOC:∠BOD=2:1,直接写出∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市元宵节灯展参观人数约为470000,将这个数用科学记数法表示为( )
A. 4.7×106 B. 4.7×105 C. 0.47×106 D. 47×104
-
科目: 来源: 题型:
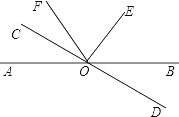
查看答案和解析>>【题目】如图,已知直线AB和CD相交于O点,∠COE=90°,OF平分∠AOE,∠COF=28°,求∠BOD的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C、D是垂足,连接CD,且交OE于点F.
(1)求证:OE是CD的垂直平分线.
(2)若∠AOB=60,请你探究OE,EF之间有什么数量关系?并证明你的结论。

-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x2﹣4x=_____.
-
科目: 来源: 题型:
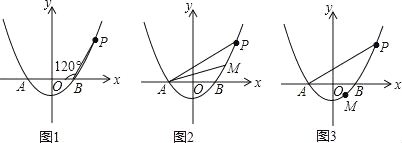
查看答案和解析>>【题目】(2016湖南省邵阳市第26题)已知抛物线y=ax2﹣4a(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.
(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为
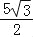 ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
相关试题

