【题目】(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系;

(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.

参考答案:
【答案】(1)∠1+∠2=∠3+∠4;(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和;(3) 60°.
【解析】试题分析:(1)根据四边形的内角和等于360°用∠5+∠6表示出∠3+∠4,再根据平角的定义用∠5+∠6表示出∠1+∠2,即可得解;
(2)从外角的定义考虑解答;
(3)根据(1)的结论求出∠MDA+∠NAD,再根据角平分线的定义求出∠ADE+∠DAE,然后利用三角形的内角和定理列式进行计算即可得解.
试题解析:
(1)∵∠3、∠4、∠5、∠6是四边形的四个内角,
∴∠3+∠4+∠5+∠6=360°.
∴∠3+∠4=360°-(∠5+∠6).
∵∠1+∠5=180°,∠2+∠6=180°,
∴∠1+∠2=360°-(∠5+∠6).
∴∠1+∠2=∠3+∠4.
(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
(3)∵∠B+∠C=240°,
∴∠MDA+∠NAD=240°.
∵AE、DE分别是∠NAD、∠MDA的平分线,
∴∠ADE=![]() ∠MDA,∠DAE=
∠MDA,∠DAE=![]() ∠NAD.
∠NAD.
∴∠ADE+∠DAE=![]() (∠MDA+∠NAD)=120°.
(∠MDA+∠NAD)=120°.
∴∠E=180°-(∠ADE+∠DAE)=60°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=x2+bx+c的图象与x轴的一个交点为B(5,0),另一个交点为A,且与y轴交于点C(0,5).
(1)求直线BC与抛物线的解析式;
(2)若点M是抛物线在x轴下方图象上的一动点,过点M作MN∥y轴交直线BC于点N,求MN的最大值;
(3)若点P是抛物线在x轴下方图象上任意一点,以BC为边作平行四边形CBPQ,当平行四边形CBPQ的面积为30时,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】因式分解:x2﹣2x+1= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知当x=﹣1时,代数式2mx3﹣3mx+6的值为7.
(1)若关于y的方程2my+n=11﹣ny﹣m的解为y=2,求n=的值;
(2)若规定[a]表示不超过a的最大整数,例如[4.3]=4,请在此规定下求[m﹣ n]的值.
n]的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.a3+a2=a5
B.a3﹣a2=a
C.a3a2=a6
D.a3÷a2=a -
科目: 来源: 题型:
查看答案和解析>>【题目】如图:在数轴上A点表示数a,B点示数b,C点表示数c,b是最小的正整数,且a、b满足|a+2|+(c﹣7)2=0.
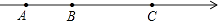
(1)a= , b= , c=;
(2)若将数轴折叠,使得A点与C点重合,则点B与数表示的点重合;
(3)点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和4个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= , AC= , BC= . (用含t的代数式表示)
(4)请问:3BC﹣2AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值. -
科目: 来源: 题型:
查看答案和解析>>【题目】“如果两个角是对顶角,那么这两个角相等”,这个命题设是______ ,结论是______ .
相关试题

