【题目】如图(1),菱形ABCD对角线AC、BD的交点O是四边形EFGH对角线FH的中点,四个顶点A、B、C、D分别在四边形EFGH的边EF、FG、GH、HE上.
(1)求证:四边形EFGH是平行四边形;
(2)如图(2)若四边形EFGH是矩形,当AC与FH重合时,已知![]() ,且菱形ABCD的面积是20,求矩形EFGH的长与宽.
,且菱形ABCD的面积是20,求矩形EFGH的长与宽.

参考答案:
【答案】(1)证明过程见解析;(2)长为8,宽为4.
【解析】
试题分析:(1)、根据菱形的性质可得出OA=OC,OD=OB,再由中点的性质可得出OF=OH,结合对顶角相等即可利用全等三角形的判定定理(SAS)证出△AOF≌△COH,从而得出AF∥CH,同理可得出DH∥BF,依据平行四边形的判定定理即可证出结论;(2)、设矩形EFGH的长为a、宽为b.根据勾股定理及边之间的关系可找出AC=![]() ,BD=
,BD=![]() ,利用菱形的性质、矩形的性质可得出∠AOB=∠AGH=90°,从而可证出△BAO∽△CAG,根据相似三角形的性质可得出
,利用菱形的性质、矩形的性质可得出∠AOB=∠AGH=90°,从而可证出△BAO∽△CAG,根据相似三角形的性质可得出![]() ,套入数据即可得出a=2b①,再根据菱形的面积公式得出a2+b2=80②,联立①②解方程组即可得出结论.
,套入数据即可得出a=2b①,再根据菱形的面积公式得出a2+b2=80②,联立①②解方程组即可得出结论.
试题解析:(1)/∵点O是菱形ABCD对角线AC、BD的交点, ∴OA=OC,OD=OB,
∵点O是线段FH的中点, ∴OF=OH.
在△AOF和△COH中,有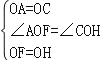 , ∴△AOF≌△COH(SAS), ∴∠AFO=∠CHO, ∴AF∥CH.
, ∴△AOF≌△COH(SAS), ∴∠AFO=∠CHO, ∴AF∥CH.
同理可得:DH∥BF. ∴四边形EFGH是平行四边形.
(2)、设矩形EFGH的长为a、宽为b,则AC=![]() . ∵
. ∵![]() =2,
=2,
∴BD=![]() AC=
AC=![]() ,OB=
,OB=![]() BD=
BD=![]() ,OA=
,OA=![]() AC=
AC=![]() .
.
∵四边形ABCD为菱形, ∴AC⊥BD, ∴∠AOB=90°. ∵四边形EFGH是矩形, ∴∠AGH=90°,
∴∠AOB=∠AGH=90°, 又∵∠BAO=∠CAG, ∴△BAO∽△CAG,
∴![]() ,即
,即![]() , 解得:a=2b①.
, 解得:a=2b①.
∵S菱形ABCD=![]() ACBD=
ACBD=![]()
![]()
![]() =20, ∴a2+b2=80②.
=20, ∴a2+b2=80②.
联立①②解得:![]() ,或
,或![]() (舍去).
(舍去).
∴矩形EFGH的长为8,宽为4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直角三角形斜边上的中线等于斜边的 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果x2+kx+1是一个完全平方式,那么k的值是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.x3+x3=x6
B.x3x9=x27
C.(x2)3=x5
D.x÷x2=x﹣1 -
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2﹣4x+2=0根的情况是( )
A.没有实数根
B.只有一个实数根
C.有两个相等的实数根
D.有两个不相等的实数根 -
科目: 来源: 题型:
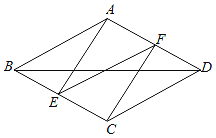
查看答案和解析>>【题目】如图,已知菱形ABCD,AB=5,对角线BD=8,作AE⊥BC于点E,CF⊥AD于点F,连接EF,求EF的长.
-
科目: 来源: 题型:
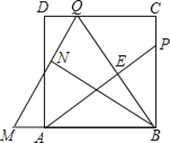
查看答案和解析>>【题目】如图,P为正方形ABCD的边BC上一动点(P与B.C不重合),点Q在CD边上,且BP=CQ,连接AP、BQ交于点E,将△BQC沿BQ所在直线对折得到△BQN,延长QN交BA的延长线于点M.
(1)求证:AP⊥BQ;
(2)若AB=3,BP=2PC,求QM的长;
(3)当BP=m,PC=n时,求AM的长。
相关试题

