【题目】已知关于x的方程x2﹣(m+2)x+2m﹣1=0.
(1)求证:此方程有两个不相等的实数根;
(2)若抛物线y=x2﹣(m+2)x+2m﹣1=0与x轴有两个交点都在x轴正半轴上,求m的取值范围;
(3)填空:若x2﹣(m+2)x+2m﹣1=0的两根都大于1,则m的取值范围是_____.
参考答案:
【答案】(1)见解析;(2) m>![]() ;(3) m>2.
;(3) m>2.
【解析】试题分析: (1)表示出根的判别式,配方后得到根的判别式大于0,进而确定出方程总有两个不相等的实数根;
(2)设抛物线y=x2﹣(m+2)x+2m﹣1=0与x轴两个交点的横坐标是x1,x2,根据两个交点都在x轴正半轴上得出x1+x2>0,x1x2>0,利用根与系数的关系列出不等式组,求解即可;
(3)设x2﹣(m+2)x+2m﹣1=0的两根是x1,x2,根据两根都大于1得出x1+x2>2,(x1﹣1)(x2﹣1)>0,根据根与系数的关系列出不等式组,求解即可.
试题解析:
(1)证明:∵△=[﹣(m+2)]2﹣4(2m﹣1)=m2+4m+4﹣8m+4=m2﹣4m+8=(m﹣2)2+4,
∵(m﹣2)2≥0,
∴(m﹣2)2+4>0,
∴无论m取何实数时,此方程都有两个不相等的实数根;
(2)解:设抛物线y=x2﹣(m+2)x+2m﹣1=0与x轴两个交点的横坐标是x1,x2,
则x1+x2=m+2,x1x2=2m﹣1.
根据题意,得![]() ,
,
解得m>![]() .
.
即m的取值范围是m>![]() ;
;
(3)解:设x2﹣(m+2)x+2m﹣1=0的两根是x1,x2,
则x1+x2=m+2,x1x2=2m﹣1.
根据题意,得![]() ,
,
解得m>2.
故答案为m>2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个数m的两个平方根分别是3a+2和a+14,求这个数m.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB=
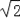 ,则GE的长为_____,并简述求GE长的思路.
,则GE的长为_____,并简述求GE长的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(
 ﹣x+1)
﹣x+1)  ,其中x为﹣1≤x≤2的整数.
,其中x为﹣1≤x≤2的整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算中,正确的是( )
A. (2x+1)(2x﹣1)=2x2﹣1B. (x+5)(x﹣6)=x2﹣x﹣30
C. (x﹣4)2=x2﹣16D. (x+2y)2=x2+2xy+4y2
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式4x2﹣16y2的结果是( )
A.(2x﹣4y)2
B.(2x﹣4y)(2x+4y)
C.4(x2﹣4y2)
D.4(x﹣2y)(x+2y) -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:(2a+1)2﹣a2= .
相关试题

