【题目】已知一个数m的两个平方根分别是3a+2和a+14,求这个数m.
参考答案:
【答案】100或400
【解析】
根据一个数的平方根互为相反数,可得这个数的平方根,再根据互为相反数的和等于0,可得平方根,再根据平方,可得这个数.
解:∵一个数的两个平方根分别是3a+2和a+14,
①(3a+2)+(a+14)=0,
a=-4,
a+14=-4+14=10,
10的平方是100.
②3a+2=a+14
a=6,
a+14=20,
202=400.
故这个数是100或400.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在3×3的正方形网格(每个小正方形的边长均为1)中有四个格点A,B,C,D,以其中一点为原点,网格线所在直线为坐标轴(水平线为横轴),建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称.
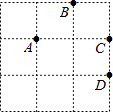
(1)原点是(填字母A,B,C,D );
(2)若点P在3×3的正方形网格内的坐标轴上,且与四个格点A,B,C,D,中的两点能构成面积为1的等腰直角三角形,则点P的坐标为(写出可能的所有点P的坐标) -
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(﹣ )﹣1﹣
)﹣1﹣ 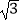 +(1﹣
+(1﹣ 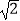 )0﹣|
)0﹣| 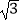 ﹣2|
﹣2|
(2)[(x+2y)(x﹣2y)﹣(x+4y)2]÷4y. -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式a3﹣4a的结果是( )
A.a(a2﹣4)
B.a(a+2)(a﹣2)
C.a(a2+2)(a2﹣2)
D.a(a2+4)(a2﹣4) -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,AB=AC,∠BAC=90°,点D在射线BC上(与B、C两点不重合),以AD为边作正方形ADEF,使点E与点B在直线AD的异侧,射线BA与射线CF相交于点G.
(1)若点D在线段BC上,如图1.
①依题意补全图1;
②判断BC与CG的数量关系与位置关系,并加以证明;
(2)若点D在线段BC的延长线上,且G为CF中点,连接GE,AB=
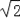 ,则GE的长为_____,并简述求GE长的思路.
,则GE的长为_____,并简述求GE长的思路.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(
 ﹣x+1)
﹣x+1)  ,其中x为﹣1≤x≤2的整数.
,其中x为﹣1≤x≤2的整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2﹣(m+2)x+2m﹣1=0.
(1)求证:此方程有两个不相等的实数根;
(2)若抛物线y=x2﹣(m+2)x+2m﹣1=0与x轴有两个交点都在x轴正半轴上,求m的取值范围;
(3)填空:若x2﹣(m+2)x+2m﹣1=0的两根都大于1,则m的取值范围是_____.
相关试题

