【题目】中央电视台举办的“中国诗词大会”节目受到中学生的广泛关注.某中学为了解该校九年级学生对观看“中国诗词大会”节目的喜爱程度,对该校九年级部分学生进行了随机抽样调查,并绘制出如图所示的两幅统计图.在条形图中,从左向右依次为:A 级(非常喜欢),B 级(较喜欢),C 级(一般),D 级(不喜欢).请结合两幅统计图,回答下列问题: 
(1)本次抽样调查的样本容量是 , 表示“D级(不喜欢)”的扇形的圆心角为°;
(2)若该校九年级有200名学生.请你估计该年级观看“中国诗词大会”节目B 级(较喜欢)的学生人数;
(3)若从本次调查中的A级(非常喜欢)的5名学生中,选出2名去参加广州市中学生诗词大会比赛,已知A级学生中男生有3名,请用“列表”或“画树状图”的方法求出所选出的2名学生中至少有1名女生的概率.
参考答案:
【答案】
(1)50;21.6
(2)解: ![]() ,
,
答:估计该年级观看“中国诗词大会”节目B 级(较喜欢)的学生人数为100.
(3)解:画树状图如下:

由树状图可以,抽取2名学生,共有20种等可能的结果,其中至少有1名女生的结果有14种,
∴P(2名学生中至少有1名女生)= ![]() =
= ![]() .
.
【解析】(1)本次抽样调查的样本容量是17÷34%=50, 表示“D级(不喜欢)”的扇形的圆心角为 ![]() ×360°=21.6°,
×360°=21.6°,
所以答案是:50,21.6;
【考点精析】通过灵活运用总体、个体、样本、样本容量和扇形统计图,掌握所要考察的全体对象叫总体,组成总体的每一个考察对象叫个体,被抽取的那部分个体组成总体的一个样本,样本中个体的数目叫这个样本的容量(样本容量没有单位);能清楚地表示出各部分在总体中所占的百分比.但是不能清楚地表示出每个项目的具体数目以及事物的变化情况即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,DE是过点A的直线,BD⊥DE于D,CE⊥DE于点E;
(1)若B、C在DE的同侧(如图所示)且AD=CE.求证:AB⊥AC;
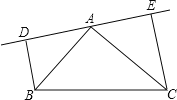
(2)若B、C在DE的两侧(如图所示),其他条件不变,AB与AC仍垂直吗?若是请给出证明;若不是,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)解不等式组
(2)解方程 .
. -
科目: 来源: 题型:
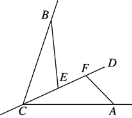
查看答案和解析>>【题目】如图,已知CA=CB,点E,F在射线CD上,满足∠BEC=∠CFA,且∠BEC+∠ECB+∠ACF=180°.
(1)求证:△BCE≌△CAF;
(2)试判断线段EF,BE,AF的数量关系,并说明理由.
-
科目: 来源: 题型:
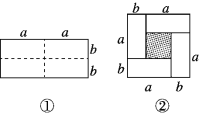
查看答案和解析>>【题目】动手操作:如图①是一个长为2a,宽为2b的长方形,沿图中的虚线剪开分成四个大小相等的长方形,然后按照图②所示拼成一个正方形.
提出问题:
(1)观察图②,请用两种不同的方法表示阴影部分的面积:_____________,_____________;
(2)请写出三个代数式(a+b)2,(a-b)2,ab之间的一个等量关系:___________________________;
问题解决:根据上述(2)中得到的等量关系,解决下列问题:已知x+y=8,xy=7,求x-y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】常用的分解因式的方法有提取公因式法、公式法及十字相乘法,但有更多的多项式只用上述方法就无法分解,如
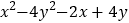 ,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了。过程为:
,我们细心观察这个式子就会发现,前两项符合平方差公式,后两项可提取公因式,前后两部分分别分解因式后会产生公因式,然后提取公因式就可以完成整个式子的分解因式了。过程为: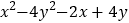 =
=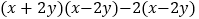 =
=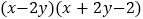
这种分解因式的方法叫分组分解法。利用这种方法解决下列问题:
(1)分解因式: ①
 ;②2x﹣2y﹣x2+y2
;②2x﹣2y﹣x2+y2(2)
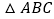 三边a,b,c 满足
三边a,b,c 满足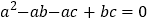 ,判断
,判断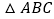 的形状.
的形状. -
科目: 来源: 题型:
查看答案和解析>>【题目】某小区为更好的提高业主垃圾分类的意识,管理处决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买3个温馨提示牌和4个垃圾箱共需580元,且每个温馨提示牌比垃圾箱便宜40元.
(1)问购买1个温馨提示牌和1个垃圾箱各需多少元?
(2)如果需要购买温馨提示牌和垃圾箱共100个,费用不超过8000元,问最多购买垃圾箱多少个?
相关试题

