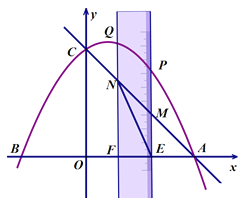
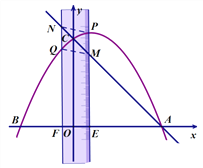
【题目】如图,已知抛物线![]() 与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
与x轴交于A、B两点(点A在点B的右侧),与y轴交于点C,有一宽度为1的刻度尺沿x轴方向平移,与y轴平行的一组对边交抛物线于点P和点Q,交直线AC于点M和点N,交x轴于点E和点F.
(1)求点A、B、C的坐标;
(2)当点M和点N都在线段AC上时,连接EN,如果点E的坐标为(4,0),求sin∠ANE的值;
(3)在刻度尺平移过程中,当以点P、Q、N、M为顶点的四边形是平行四边形时,求点N的坐标.
参考答案:
【答案】(1)A(5,0)、B(-3,0)、C(0,5);(2) ![]() ;(3) 点N的坐标为(2,3)或(2+
;(3) 点N的坐标为(2,3)或(2+![]() ,3﹣
,3﹣![]() )或(2﹣
)或(2﹣![]() ,3+
,3+![]() )
)
【解析】(1)令y=0得: ![]() =0,解得x=5或x=-3.
=0,解得x=5或x=-3.
∵点A在点B的右侧,
∴点A、B的坐标分为(5,0)、(-3,0).
当x=0时,y=5,
∴点C的坐标为(0,5).………………………………………………3分
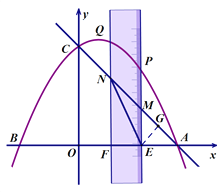 (2)如图1,作EG⊥AC,垂足为点G.
(2)如图1,作EG⊥AC,垂足为点G.
∵点E的坐标为(4,0),
∴OE=4.
∵OA=OC=5,
∴AE=1,∠OAC=45°.
∴AF=FN=2,GE=AEsin45°=![]() .………………5分
.………………5分
![]() 在Rt△EFN中,依据勾股定理可知NE=
在Rt△EFN中,依据勾股定理可知NE=![]() =
=![]() =
=![]() .………………6分
.………………6分
∴sin∠ANE=![]() =
=![]() =
=![]() .……………………7分
.……………………7分
(3)设直线AC的函数表达式为y=kx+b.
 将点A和点C的坐标代入得:
将点A和点C的坐标代入得: ![]() ,
,
解得k=﹣1,b=5.
∴直线AC的函数表达式为y=﹣x+5.………………9分
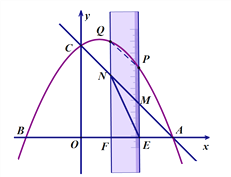
①当MN为边时,如图2所示:
![]() 设点Q(n,
设点Q(n, ![]() ),则点P(n+1,
),则点P(n+1, ![]() ),点N(n,﹣n+5)M(n+1,-n+4).
),点N(n,﹣n+5)M(n+1,-n+4).
∵QN=PM
∴![]() ,解得n=2.
,解得n=2.
 ∴点N的坐标为(2,3).………………………………10分
∴点N的坐标为(2,3).………………………………10分
当MN是平行四边形的对角线时,如图3所示:
设点F的坐标为(m,0),
则N(m,﹣m+5),M(m+1,﹣m+4),
![]() Q(m,
Q(m, ![]() ),P(m+1,
),P(m+1, ![]() ).
).
∵QN = PM,
∴![]() ,解得m=2±
,解得m=2±![]() .
.
∴点N的坐标为(2![]() ,3﹣
,3﹣![]() )或(2﹣
)或(2﹣![]() ,3+
,3+![]() ).
).
综上所述,以点P、Q、N、M为顶点的四边形是平行四边形时,点N的坐标为(2,3)或(2![]() ,3﹣
,3﹣![]() )或(2﹣
)或(2﹣![]() ,3+
,3+![]() ).…………………………12分
).…………………………12分
-
科目: 来源: 题型:
查看答案和解析>>【题目】利用复印机的缩放功能,将原图中边长为5厘米的一个等边三角形放大成边长为20厘米的等边三角形,那么放大前后的两个三角形的周长比是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】要使方程x(x2+a)+3x-2b=x3+5x+4成立,则a,b的值分别是( )
A. 2,2 B. -2,-2 C. 2,-2 D. -2,2
-
科目: 来源: 题型:
查看答案和解析>>【题目】化简xy[xy(xy-1)+1]的结果为( )
A. x2y2-xy+1 B. x3y3-x2y2+xy
C. x3y3-xy+1 D. x3y3+xy+1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在反比例函数
 (x>0)的图象上,有点P1、P2、P3、P4 , 它们的横坐标依次是1、2、3、4,分别过这些点作x轴与y轴的垂线,若图中所构成的阴影部分的面积从左到右依次为S1、S2、S3 , 则S1+S2+S3= .
(x>0)的图象上,有点P1、P2、P3、P4 , 它们的横坐标依次是1、2、3、4,分别过这些点作x轴与y轴的垂线,若图中所构成的阴影部分的面积从左到右依次为S1、S2、S3 , 则S1+S2+S3= . 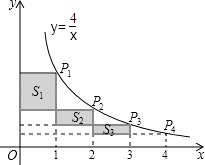
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,矩形
 的边OA、OC分别落在x轴、y轴上,O为坐标原点,且OA=8,OC=4,连接AC,将矩形OABC对折,使点A与点C重合,折痕ED与BC交于点D,交OA于点E,连接AD,如图①.
的边OA、OC分别落在x轴、y轴上,O为坐标原点,且OA=8,OC=4,连接AC,将矩形OABC对折,使点A与点C重合,折痕ED与BC交于点D,交OA于点E,连接AD,如图①.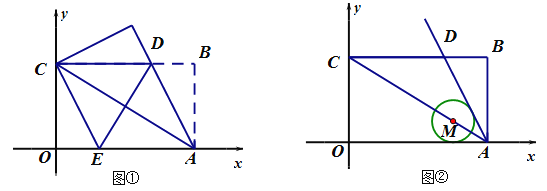
(1)求点
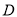 的坐标和
的坐标和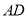 所在直线的函数关系式;
所在直线的函数关系式;(2)
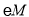 的圆心
的圆心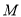 始终在直线
始终在直线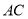 上(点
上(点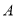 除外),且
除外),且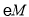 始终与x轴相切,如图②.
始终与x轴相切,如图②.①求证:
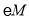 与直线AD相切;
与直线AD相切;②圆心
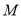 在直线AC上运动,在运动过程中,能否与y轴也相切?如果能相切,求出此时
在直线AC上运动,在运动过程中,能否与y轴也相切?如果能相切,求出此时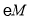 与x轴、y轴和直线AD都相切时的圆心
与x轴、y轴和直线AD都相切时的圆心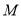 的坐标;如果不能相切,请说明理由.
的坐标;如果不能相切,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】甩不掉的21:
(1)观察:3×7=21,13×17=221,23×27=621,33×37=1221…,请研究其中的规律,并用代数式表示这一规律;
(2)利用你找到的规律计算93×97;(写出过程)
相关试题

